Triangles isométriques

[lapras]

Bonsoir,

On se donne 4 triangles rectangles isométriques. On prend l'un d'entre eux et on le coupe en deux triangles avec la hauteur issue de l'angle droit. Puis on recommence cette opération avec tous les triangles rectangles restant. Montrer qu'on aura toujours au moins deux triangles isométriques.

C'est un bel exo :we: (mais pas extremement difficile)

[Imod]

Les quatre premiers triangles sont rectangles et isométriques : ça a l'air amusant :we:

Ce qui est sûr c'est que tous les triangles sont semblables .

Imod

[lapras]

Oui rectangles évidemment, désolé pour l'erreur j'ai modifié le sujet.
Effectivement, une premiere piste c'est que les triangles sont homothétiques.

[ffpower]

Je crois que je l ai(il m a bien amusé)
Alors,d apres la remarque d Imod,tous les triangles ont meme proprtions
A chaque etape,on remplace un triangle par 2 triangles plus petit.L un a eu les dimensions multipliées par un certain a,l autre a eu ces dimensions multipliees par un certain b,ou a et b sont 2 reels fixés(qui doivent etr lié a la tangeante d un angle ou un truc comme ca).

Je dit qu un triangle est de type (i,j) si pour l obtenir on a multiplié les dimensions d un des triangles initiaux i fois par a et j fois par b.Ainsi avec cette notation,l operation que l on effectue est la suivante:On part de 4 triangles de type (0,0) et a chaque etape on remplace un triangle de type (i,j) par un triangle de type (i+1,j) et un triangle de type (i,j+1).Et on veut donc montrer qu il y a forcément au moins 2 triangles de meme type.

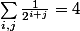
Et enfin,je dit qu un triangle de type (i,j) a une "masse" de 1/2^(i+j).Ainsi il y a conservation de cette masse(a chaque fois on remplace un triangle par 2 triangles 2 fois moins lourds).donc la somme des masses vaut 4.Or,si tous les triangles étaient de type distincts,la somme des masses devrait etre strictement inferieure a ,ce n est donc pas possible..

[lapras]

Bravo c'est exactement ca !
Il est assez "naturel" de chercher un invariant dans cet exercice et ici c'est un systeme de "poids" (bon un peu tordu mais bon...) Ce qui est bien c'est que la somme de ces poids - qui est tjrs égale à 4- ne peut etre égale à quatre que faisant un nombre infini d'opération (somme des 1/2^i)....
:happy2:

[ffpower]

au depart j essayais juste avec les aires mais ca marchait pas bien^^.mais t exagere qd meme lol,il était pas si facile que ca quand meme,heureusement que j avais vu cette idee ya pas longtemps sur un exercice sur le solitaire(que je posterai bientot^^)

[Imod]

En fait facile ne veut rien dire , il faudrait donc l'éviter ( ce que je ne fais pas :zen: ). est évidemment irrationnel , il a poutant fallu des siècles pour le montrer et a plongé les Pythagoriciens dans un embarras inimaginable .

Mais bon , quand on a la solution , on a du mal à admettre que les autres ne suivent pas !

Imod

[lapras]

Je n'ai jamais dit que ce problème était facile. J'ai dit que parmis les problemes que je connais sur les invariants, il n'est pas "extremement" difficile". Et quand j'ai dit que c'était "naturel" , je parlais de chercher un invariant, pas de trouver un systeme de poids (c'est déja moins naturel !) et puis c'est subjectif.
Sinon ffpower, j'ai aussi cherché du coté des aires mais ca n'a pas l'air de marcher...

[Imod]

Il faut dire qu'à partir du moment où on l'a catalogué dans un problème d'invariant , on a déjà fait un grand pas :zen: Les plus beaux problèmes font appel aux domaines auxquels on ne pense pas ou peu .

Imod

[Zweig]

C'est quoi ce système de poids ? Je ne l'ai jamais vu auparavent ... Un autre problème qui implique cette technique ?

[lapras]

Je crois que dans Engel il doit y avoir des exos de ce type (chapitre invariants) : c'est pour ca que j'ai pensé au poids dans ce probleme.