Un triangle et des certains cercles
Olympiades mathématiques, énigmes et défis
-
hammana
- Membre Relatif
- Messages: 477
- Enregistré le: 24 Avr 2012, 20:26
-
 par hammana » 07 Avr 2013, 10:12
par hammana » 07 Avr 2013, 10:12
chan79 a écrit:Juste pour mettre le dessin
Quelle est la question ?
La figure est simple à réaliser. On commence par un triangle de côtés 2, 3 et 4.

Uploaded with
ImageShack.us
Si le triangle ABC est quelconque il me semble impossible de dessiner une figure comme celle de Chan. La question pourrit être "A quelle condition doit satisfaire le triangle ABC pour qu'une telle figure soit possible"
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 07 Avr 2013, 10:19
par Imod » 07 Avr 2013, 10:19
Comme le fait remarquer Chan la condition nécessaire et suffisante est que le triangle soit homothétique à (2,3,4) .
Imod

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Avr 2013, 10:29
par chan79 » 07 Avr 2013, 10:29
Imod a écrit:Comme le fait remarquer Chan la condition nécessaire et suffisante est que le triangle soit homothétique à (2,3,4) .
Imod
le cosinus de
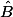
doit être égal à

et celui de
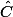
à

-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 07 Avr 2013, 14:45
par Dacu » 07 Avr 2013, 14:45
chan79 a écrit:Juste pour mettre le dessin
Quelle est la question ?
La figure est simple à réaliser. On commence par un triangle de côtés 2, 3 et 4.

Uploaded with
ImageShack.us
Bonjour!
Correctement!Quelle est la valeur de
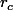
, où
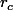
est le rayon de l'un de ces cercles egaux?
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Avr 2013, 17:12
par chan79 » 07 Avr 2013, 17:12
Dacu a écrit:Bonjour!
Correctement!Quelle est la valeur de
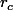
, où
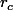
est le rayon de l'un de ces cercles egaux?
Cordialement!
Soit un triangle ABC, [BC] étant le plus grand côté.
Il est nécessaire que cos(B)=11/16 et cos(C)=7/8 pour que la figure soit réalisable.
si on pose a=BC, on a, en évaluant BC en fonction de r:
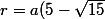}{16})
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 07 Avr 2013, 19:01
par LeJeu » 07 Avr 2013, 19:01
chan79 a écrit:Juste pour mettre le dessin
Quelle est la question ?
La figure est simple à réaliser. On commence par un triangle de côtés 2, 3 et 4.
Désolé, mais il me semble que mon triangle était aussi elligilble, en prenant le triangle extérieur si tu préfères

Ce qui doit vouloir dire que ton pb doit avoir un tas de solutions ( que les contraintes ne sont pas assez fortes...)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Avr 2013, 19:14
par chan79 » 07 Avr 2013, 19:14
LeJeu a écrit:Désolé, mais il me semble que mon triangle était aussi elligilble, en prenant le triangle extérieur si tu préfères
Ce qui doit vouloir dire que ton pb doit avoir un tas de solutions ( que les contraintes ne sont pas assez fortes...)
Salut
j'avais compris que le cercle le plus proche de A devait être tangent à ses deux voisins et aux deux côtés, comme quoi il faut bien poser le problème.
je vais regarder de nouveau :zen:
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 07 Avr 2013, 19:17
par LeJeu » 07 Avr 2013, 19:17
chan79 a écrit:Salut
j'avais compris que le cercle le plus proche de A devait être tangents à ses deux voisins
je vais regarder de nouveau :zen:
Toutes mes excuses chan
Je voulais adresser ma réponse à Dacu !!!!
Ta réponse est évidemment ok pour le dessin présenté par Dacu
je venais juste
lui dire que son problème était posé complètement de traviole
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 08 Avr 2013, 06:26
par Dacu » 08 Avr 2013, 06:26
LeJeu a écrit:Toutes mes excuses chan
Je voulais adresser ma réponse à Dacu !!!!
Ta réponse est évidemment ok pour le dessin présenté par Dacu
je venais juste lui dire que son problème était posé complètement de traviole
Bonjour!
Ce qui est de traviole???!!! :doh:
------------------------------------------
Vôtre dessin est d'un autre problème!!!IMod bien mieux compris comment faire le dessin!!!!!!!!!
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités


