Toutankhamon

par **Zweig** » 15 Déc 2010, 20:01

Salut,

Voici un joli problème (ceux qui sont sur mon Fesse de bouc, merci de ne pas dévoiler les astuces, à moins que vous ayez la solution, bien sûr :lol3:). J'ai un peu la flemme de le latexiser en français, ne m'en veuillez pas.

par **nodjim** » 15 Déc 2010, 20:19

Let il be. let it be.

par **Ben314** » 16 Déc 2010, 17:03

par **Zweig** » 16 Déc 2010, 17:09

Joli ... Il existe sinon une démonstration purement géométrique (celle que j'attendais plutôt). Je laisse chercher.

par **hydroemir** » 16 Déc 2010, 17:14

(x,y,z)=( :mur: , :cry: , :bad: )

par **Lostounet** » 16 Déc 2010, 17:40

Triplet Pythagoricien?

par **Lostounet** » 16 Déc 2010, 17:40

Salut!

Triplet Pythagoricien?

par **Ben314** » 16 Déc 2010, 18:20

Zweig a écrit:Joli ... Il existe sinon une démonstration purement géométrique (celle que j'attendais plutôt). Je laisse chercher.

Essaye de comprendre bien proprement ce que dit ta "preuve purement géométrique" et tu verra que...

par **Anonyme** » 17 Déc 2010, 17:26

Donc Ben tu as trouve la demo geometrique puis tu as efface la partie geometrique pour rendre la preuve parachutee ?

par **Ben314** » 17 Déc 2010, 17:52

Qmath a écrit:Donc Ben tu as trouve la demo geometrique puis tu as efface la partie geometrique pour rendre la preuve parachutee ?

C'est un peu ça...

par **Anonyme** » 18 Déc 2010, 19:28

Une aide serait la bienvenue :hein:

par **Anonyme** » 19 Déc 2010, 19:07

Alors ? :dodo:

par **Zweig** » 19 Déc 2010, 19:34

9, 16, 25 font penser au triangle égyptien (d'où le titre ...), càd le triangle rectangle de côté 3, 4 et 5 (hypothénuse).

Maintenant la première et la dernière relation font penser à Al-Kashi et la deuxième à Pythagore. Etant donné que la somme voulue est une somme de 3 nombres, cela peut être l'aire de ce fameux triangle égyptien, morcelé en 3 parties compte tenu des relations du système...

Voilà.

par **Anonyme** » 19 Déc 2010, 20:17

Donc on construit un triangle rectangle (3,4,5).

Et a partir de chaque cote du triangle on construit un autre.

Au cote de longueur 3 correspond un triangle rectangle de cotes

et

.
Au cote de longueur 4 correspond un triangle de cotes

et

et l'angle entre eux est de 120 degrés.

Au cote de longueur 5 correspond un triangle de cotes

et

et l'angle entre eux est de 150 degrés.

Maintenant 150+120+90=360 donc on doit pouvoir trouve un point O a lintérieur ABC (le triangle égyptien en A) tel que

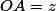
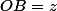
et

.

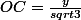
C'est ce que j'ai trouve pour l'instant

par **Zweig** » 19 Déc 2010, 20:28

C'est ça, maintenant calcule de deux manières différentes l'aire de ABC.

Toutankhamon

Toutankhamon

Qui est en ligne