[MP] Topologie.
Olympiades mathématiques, énigmes et défis
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 23 Nov 2012, 20:16
par vincentroumezy » 23 Nov 2012, 20:16
Bonsoir à tous.
Soit

de degré supérieur ou égal à 2.
On définit, pour z complexe,
))
par u0(z)=z et pour n positif,
=P(u_n(z)))
.
Mq K={z de C tels que un(z) est bornée} est compact.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Nov 2012, 16:07
par Nightmare » 24 Nov 2012, 16:07
Hello,
Si |un(z)| est majorée par M, M ne dépend que de P. Alors K s'écrit comme intersection dénombrable sur n des z tels que |un(z)| soit majoré par M qui est donc compact comme intersection de compacts.
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 24 Nov 2012, 16:43
par vincentroumezy » 24 Nov 2012, 16:43
Ah ouais, joli.
J'étais parti sur un truc plus basique, comme C est de dimension finie, il suffit de prouver que K est fermé et borné.
Borné; par l'absurde.
Fermé: pas encore cherché.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Nov 2012, 16:46
par Nightmare » 24 Nov 2012, 16:46
On peut faire comme ça aussi, pour le caractère fermé, on peut examiner ce que vaut P(K) et P-1(K)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 24 Nov 2012, 16:58
par ffpower » 24 Nov 2012, 16:58
Nightmare a écrit:Si |un(z)| est majorée par M, M ne dépend que de P
Que signifie cette phrase?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Nov 2012, 17:01
par Nightmare » 24 Nov 2012, 17:01
ffpower > C'est un peu confus dit comme ça en effet.
La suite (un(z)) est construite à partir de z, son premier terme et P.
Si elle est bornée et si M est une borne, a priori M dépend de z et de P. On peut montrer facilement qu'il existe une borne M qui ne dépend que de P et non de z, c'est ce que je voulais dire.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Nov 2012, 17:50
par Nightmare » 24 Nov 2012, 17:50
Bon, ça fait un moment que je cherche des applications d'un tel résultat, et après avoir galéré je suis finalement tombé sur les ensembles de Julia dont l'étude est très intéressante.
Pour rester au niveau de l'exercice donné, il peut être intéressant de chercher plus de propriétés de K : Peut-il être connexe? A-t-il beaucoup de points isolés?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 24 Nov 2012, 18:18
par vincentroumezy » 24 Nov 2012, 18:18
C'est un exo d'oral d'Ulm 2008, et justement la deuxième question est: est-ce connexe par arc ?
(je ne sais pas ce que c'est).
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Nov 2012, 22:37
par Doraki » 24 Nov 2012, 22:37
Nightmare a écrit:Hello,
Si |un(z)| est majorée par M, M ne dépend que de P. Alors K s'écrit comme intersection dénombrable sur n des z tels que |un(z)| soit majoré par M qui est donc compact comme intersection de compacts.
Oui mais l'ensemble en question est a priori la réunion dénombrable de ces compacts lorsqu'on prend M de plus en plus grand.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Nov 2012, 01:00
par Nightmare » 25 Nov 2012, 01:00
Je ne comprends pas ta remarque Doraki. M est fixé, choisi par exemple tel que dès que |x| > M, |P(x)| > 2M
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Nov 2012, 01:30
par Doraki » 25 Nov 2012, 01:30
Dans ta preuve tu as essentiellement montré que l'ensemble des z qui génèrent une suite bornée par M est compact.
C'est vrai, mais nous on veut les z qui génèrent une suite bornée par n'importe quoi.
En fait c'était en réaction à ton "M ne dépend que de P" (on comprend plus, M il est fixé ou alors il dépend d'un truc ? si il dépend de P, comment on le choisit ? en quoi P influe ?)
Ah ffpower avait aussi fait la remarque.
J'avais pas vu que après tu as dit "on peut montrer facilement qu'il existe M tel que pour tout z, si la suite générée par z est bornée alors elle est bornée par M"
Enfin pour moi c'est quand même la moitié de l'exo.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 25 Nov 2012, 01:54
par Judoboy » 25 Nov 2012, 01:54
Doraki a écrit:J'avais pas vu que après tu as dit "on peut montrer facilement qu'il existe M tel que pour tout z, si la suite générée par z est bornée alors elle est bornée par M"
Enfin pour moi c'est quand même la moitié de l'exo.
Oui je veux bien des pistes pour montrer ça

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Nov 2012, 02:16
par Doraki » 25 Nov 2012, 02:16
Ben tu dois montrer qu'il existe M tel que |z| > M => P^n(z) tend vers l'infini. Or, pour |z| grand, |P(z)| ~ |a z ^d| (d >= 2 est le degré de P), donc tu devrais pouvoir y arriver.
Si t'aimes bien la sphère de Riemann, tu montres que l'infini est un point fixe attracteur de n'importe quel polynôme.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 25 Nov 2012, 02:28
par Judoboy » 25 Nov 2012, 02:28
Oulah je m'embrouille.
Si on montre que K est borné (ce qui est très facile par l'absurde) on a directement cette propriété en fait non ? Vu que tous les éléments de Un(z) doivent être dans K dès que z est dans K...
Par contre composer des équivalents on m'a trop hurlé que c'était illégal pour que je le fasse :)
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 25 Nov 2012, 02:46
par Judoboy » 25 Nov 2012, 02:46
Après l'ensemble est pas connexe ; en gros il a une tronche qui dépend de la position des racines dans le plan complexe, si on éloigne trop les racines les parties du plan entre les racines sont plus dans K alors que par exemple les racines sont dans K si 0 est racine de P.
On prend par rxemple P = 5X(X-2)
0 et 2 appartiennent à K mais aucun élément de la sphère unité n'est dans K, donc K n'est pas connexe.
Je sais pas trop si on peut obtenir un résultat sympa en fonction de la tête du polynôme.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Nov 2012, 09:02
par Doraki » 25 Nov 2012, 09:02
Judoboy a écrit:Oulah je m'embrouille.
Si on montre que K est borné (ce qui est très facile par l'absurde)
Ben je n'ai fait que traduire "K est borné" en termes concrets ... c'est quoi ta preuve que K est borné ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 25 Nov 2012, 11:17
par Judoboy » 25 Nov 2012, 11:17
Doraki a écrit:Ben je n'ai fait que traduire "K est borné" en termes concrets ... c'est quoi ta preuve que K est borné ?
Si on prend |z| trop grand |Un(z)| tend vers l'infini.
Si on prend r le max des modules des racines de P, ça doit marcher avec |z| = (3r+2) si |an|>=1 et |z| = (3r+2)/|an| si |an|<1. (an est le coef dominant de P bien sûr).
Ca doit marcher avec des normes bien moins grandes mais j'ai pas le temps de chercher plus fin là.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Nov 2012, 13:34
par Nightmare » 25 Nov 2012, 13:34
Doraki a écrit:Enfin pour moi c'est quand même la moitié de l'exo.
Je suis d'accord, c'est pour ça que j'ai précisé ensuite la preuve de l'existence de M dans mon message.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Nov 2012, 14:11
par Nightmare » 25 Nov 2012, 14:11
Judoboy a écrit:Après l'ensemble est pas connexe ; en gros il a une tronche qui dépend de la position des racines dans le plan complexe, si on éloigne trop les racines les parties du plan entre les racines sont plus dans K alors que par exemple les racines sont dans K si 0 est racine de P.
On prend par rxemple P = 5X(X-2)
0 et 2 appartiennent à K mais aucun élément de la sphère unité n'est dans K, donc K n'est pas connexe.
Je sais pas trop si on peut obtenir un résultat sympa en fonction de la tête du polynôme.
Si tout ceci t'intéresse, tape "ensembles de Julia remplis" sous google (ou "filled Julia Set" en anglais) et tu trouveras de nombreux résultats (pas toujours simples à démontrer).
On trouve par exemple le résultat suivant :
Pour P=X²+a et
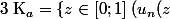)\;bornee\})
. Alors Ka est connexe si et ss'il contient 0. Sinon, il est isomorphe à un Cantor
C'est quand même assez fort comme résultat.
On peut alors s'intéresser à l'ensemble de tous les a pour lesquels Ka est connexe, cet ensemble est nommé "ensemble de Mandelbrot" par les mathématiciens et a aussi de nombreuses propriétés intéressantes. Il est par exemple connexe.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 25 Nov 2012, 18:19
par ffpower » 25 Nov 2012, 18:19
Je propose l'exercice suivant:
1) Quels sont les polynomes P tels que K=disque unite
2) Quels sont les polynomes P tels que K=[-1,1]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
. Alors Ka est connexe si et ss'il contient 0. Sinon, il est isomorphe à un Cantor