A²+1=2*b²
19 messages
- Page 1 sur 1
a²+1=2*b²
Bonjour à tous.
Résoudre dans N cette équation.
C'est sûrement connu. J'imagine qu'il existe peut être une manière générale de résoudre, quand c'est possible: ka²+b=jc² avec k,b et j donnés.
Résoudre dans N cette équation.
C'est sûrement connu. J'imagine qu'il existe peut être une manière générale de résoudre, quand c'est possible: ka²+b=jc² avec k,b et j donnés.
Salut,
Cherche "Equation de Pell-Fermat" (celles de la forme x²-dy²=+-1 avec ici d=2) et tu devrait trouver ton bonheur.
On peut aussi les trouver sans connaitre toute la théorie : on utilise la "méthode de descente" de Fermat, c'est à dire que, partant d'une solution (x,y) on montre que l'on peut en trouver une autre (x',y') "plus petite" (sous certaines conditions...)
Cherche "Equation de Pell-Fermat" (celles de la forme x²-dy²=+-1 avec ici d=2) et tu devrait trouver ton bonheur.
On peut aussi les trouver sans connaitre toute la théorie : on utilise la "méthode de descente" de Fermat, c'est à dire que, partant d'une solution (x,y) on montre que l'on peut en trouver une autre (x',y') "plus petite" (sous certaines conditions...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
On peut aussi les trouver sans connaitre toute la théorie : on utilise la "méthode de descente" de Fermat, c'est à dire que, partant d'une solution (x,y) on montre que l'on peut en trouver une autre (x',y') "plus petite" (sous certaines conditions...)
oui, c'est avec cette méthode que j'avais trouvé a=1, b=1
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Par exemple, "à la main",
Tu peut montrer que, si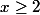 et
et 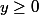 vérifient
vérifient 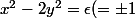) ,
,
alors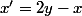 et
et 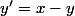 sont
sont 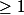 , vérifient
, vérifient 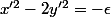 et
et 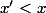 .
.
A force de "descendre", on fini par tomber sur une solution telle que et
et 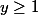 c'est à dire sur la solution "triviale"
c'est à dire sur la solution "triviale" 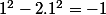 (qui, si on itère une fois de plus le procéssus donne
(qui, si on itère une fois de plus le procéssus donne 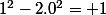 )
)
cela permet en "remontant" de trouver toutes les autres solutions.
Tu peut montrer que, si
alors
A force de "descendre", on fini par tomber sur une solution telle que
cela permet en "remontant" de trouver toutes les autres solutions.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pas à ma conaissance (i.e. je ne connais pas de théorie générale simple, mais il y a forcément des cas particuliers où c'est faisable)nodjim a écrit:Je ne connaissais pas. Je trouve ça intéressant. C'est du bezout, mais avec des carrés. On peut aussi avec des cubes ou des puissances supérieures ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Sur cette équation particulière,
les solutions vont être essentiellement données par des approximations de racine(2) (a/b vaut presque racine(2)).
Quand tu es face à 2b²-a² = 1,
il y a une solution (a=1, b=1), et sinon, tu peux déduire que les autres solutions sont telles que a>b (parceque si b=a, ça fait a², qui est trop grand)
Du coup tu remplaces a par a+b' et tu recommences.
Le truc bien quand t'es en degré 2, c'est que tu vas forcément finir par retomber sur l'équation de départ (et en fait, les transformations que tu fais peuvent se lire sur le développement en fraction continue de racine(2), qui est lui aussi périodique)
Dès que tu es en degré 3, même si tu appliques ce procédé, tu verras vite que les coefficients devant a^3, a²b, ab², b^3 vont pas être bornés et que tu vas jamais pouvoir retomber sur une équation déjà connue (et ça devrait être pareil pour le développement en fraction continue)
Une façon un peu plus élaborée de décrire ce qui se passe est de dire que l'équation équivaut à trouver les éléments de Z[sqrt(2)] de norme -1. Si on en a un (par exemple 1+-racine(2)), les autres sont obtenus en le multipliant par un élément de norme 1.
Et on peut étudier la structure du groupe des éléments de norme 1 de Z[sqrt(2)] et voir qu'il est isomorphe à (Z/2Z) * Z
(on a -1 qui est d'ordre 2, et 3+-2racine(2) pour la composante infinie)
les solutions vont être essentiellement données par des approximations de racine(2) (a/b vaut presque racine(2)).
Quand tu es face à 2b²-a² = 1,
il y a une solution (a=1, b=1), et sinon, tu peux déduire que les autres solutions sont telles que a>b (parceque si b=a, ça fait a², qui est trop grand)
Du coup tu remplaces a par a+b' et tu recommences.
Le truc bien quand t'es en degré 2, c'est que tu vas forcément finir par retomber sur l'équation de départ (et en fait, les transformations que tu fais peuvent se lire sur le développement en fraction continue de racine(2), qui est lui aussi périodique)
Dès que tu es en degré 3, même si tu appliques ce procédé, tu verras vite que les coefficients devant a^3, a²b, ab², b^3 vont pas être bornés et que tu vas jamais pouvoir retomber sur une équation déjà connue (et ça devrait être pareil pour le développement en fraction continue)
Une façon un peu plus élaborée de décrire ce qui se passe est de dire que l'équation équivaut à trouver les éléments de Z[sqrt(2)] de norme -1. Si on en a un (par exemple 1+-racine(2)), les autres sont obtenus en le multipliant par un élément de norme 1.
Et on peut étudier la structure du groupe des éléments de norme 1 de Z[sqrt(2)] et voir qu'il est isomorphe à (Z/2Z) * Z
(on a -1 qui est d'ordre 2, et 3+-2racine(2) pour la composante infinie)
nodjim a écrit:Je ne connaissais pas. Je trouve ça intéressant. C'est du bezout, mais avec des carrés. On peut aussi avec des cubes ou des puissances supérieures ?
Il existe un bouquin (en ebook si tu veux en avoir un aperçu aussi) qui traite des équation de Pell-Fermat classiques + aux puissances supérieures.
http://www.amazon.com/Pells-Equation-Problem-Books-Mathematics/dp/144193040X/ref=sr_1_1?s=books&ie=UTF8&qid=1286686028&sr=1-1
Salut,
Si (x,y) est une solution, vérifie que
x'=(2a-1)x-(2a-2)y
y'=-2a.x+(2a-1)y
est une solution "plus petite" que (x,y)...
Ou, si tu préfère "monter", partant de x0=1 ; y0=1, construit
x(n+1)=(2a-1)xn+(2a-2)yn
y(n+1)=2a.xn+(2a-1)yn
et tu aura ainsi toutes les solutions.
Si (x,y) est une solution, vérifie que
x'=(2a-1)x-(2a-2)y
y'=-2a.x+(2a-1)y
est une solution "plus petite" que (x,y)...
Ou, si tu préfère "monter", partant de x0=1 ; y0=1, construit
x(n+1)=(2a-1)xn+(2a-2)yn
y(n+1)=2a.xn+(2a-1)yn
et tu aura ainsi toutes les solutions.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est bien ça. Cette question vient de la comparaison entre les différentes solutions de l'équation de Pell-Fermat a²-nb²=+-1 et de l'algorithme ordinaire du calcul d'une racine carrée:
1) Pell-Fermat: parmi la série de solutions, il y a cette série: a²-nb²=-+1 puis (a²+nb²)²-n(2ab)²=+1
qui consiste à transformer le couple (a,b) en celui ci (a²+nb², 2ab) qui est le carré du précédent.
2) L'algorithme du calcul de la racine carrée: ((n/2)+n/(n/2))/2. Le premier résultat est toujours un carré. Les autres résultats s'obtiennent en transformant un rapport a/b en ((a/b)+n/(a/b))/2 qui revient à passer du couple (a,b) au couple (a²+nb², 2ab). C'est à dire qu'il s'agit du même algorithme que le précédent. Le résultat a²-+nb², qui est la différence entre la racine de n et le rapport a/b est un carré de carré de carré.... alors que l'équation de Pell Fermat donne toujours 1 comme différence.
Tout ça pour dire que si on veut calculer avec beaucoup de précision une racine carrée, c'est mieux de chercher la solution a²-nb²=+-1.
1) Pell-Fermat: parmi la série de solutions, il y a cette série: a²-nb²=-+1 puis (a²+nb²)²-n(2ab)²=+1
qui consiste à transformer le couple (a,b) en celui ci (a²+nb², 2ab) qui est le carré du précédent.
2) L'algorithme du calcul de la racine carrée: ((n/2)+n/(n/2))/2. Le premier résultat est toujours un carré. Les autres résultats s'obtiennent en transformant un rapport a/b en ((a/b)+n/(a/b))/2 qui revient à passer du couple (a,b) au couple (a²+nb², 2ab). C'est à dire qu'il s'agit du même algorithme que le précédent. Le résultat a²-+nb², qui est la différence entre la racine de n et le rapport a/b est un carré de carré de carré.... alors que l'équation de Pell Fermat donne toujours 1 comme différence.
Tout ça pour dire que si on veut calculer avec beaucoup de précision une racine carrée, c'est mieux de chercher la solution a²-nb²=+-1.
Juste un petit mot pour signaler qu'au niveau "culture générale", lorsque tu parle pour approximer racine(d) de "passer" de (a,b) à (a²+nb²,2ab), on peut aussi le voir comme une application de la méthode des tangentes de Newton qui dit que, sous certaines hypothèses (vérifiées dans le cas présent), pour approximer une solution d'une équation f(x)=0, il faut considérer la suite U(n+1)=Un-f(Un)/f'(Un).
Si on prend f(x)=x²-d (=> f(x)=0 a pour solutions +-racine(d)) on tombe sur U(n+1)=(Un²+d)/(2Un) qui, si Un=a/b dit que U(n+1)=(a²+nb²)/(2ab).
Je fait cette remarque principalement du fait que, à mon sens, la méthode "équation de Pell-Fermat" consiste plutôt à déterminer les fractions a/b qui apparaissent lorsque l'on évalue la fraction continue de racine(d) et que, dans ce cas, on obtient beaucoup plus de fractions a/b que lorsque l'on utilise la méthode de Newton (par contre, si on prend pour U0 le nombre entier suivant racine(d), les fraction obtenues par la méthode de Newton font toutes parti des fraction obtenues par le développement en fraction continue)
Si on prend f(x)=x²-d (=> f(x)=0 a pour solutions +-racine(d)) on tombe sur U(n+1)=(Un²+d)/(2Un) qui, si Un=a/b dit que U(n+1)=(a²+nb²)/(2ab).
Je fait cette remarque principalement du fait que, à mon sens, la méthode "équation de Pell-Fermat" consiste plutôt à déterminer les fractions a/b qui apparaissent lorsque l'on évalue la fraction continue de racine(d) et que, dans ce cas, on obtient beaucoup plus de fractions a/b que lorsque l'on utilise la méthode de Newton (par contre, si on prend pour U0 le nombre entier suivant racine(d), les fraction obtenues par la méthode de Newton font toutes parti des fraction obtenues par le développement en fraction continue)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
