bon je commence , je termine pas cette nuit le désavantage de ma demo est qu'elle est longue (en plus d'être particulièrement moche)
je terminerai demain normalement
( ...pour ce qui est des points a) et b) ils sont inutiles mais vus qu'ils sont courts je les place, c'est pas ça qui va rallonger )
EnoncéOn se place dans ZC
Etant donné E un ensemble quelconque, il existe une application

vérifiant la propriété suivante:

,

,
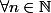
,

,
=u_n)
en notant
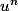
la suite
 Démonstration
Démonstration a)Cas de l'ensemble vide
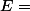
Dans ce cas il n'existe pas d'application de
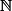
vers E
effectivement il n'existe pas d'application d'un ensemble non vide vers un ensemble vide
par conséquent
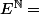
Or par contre il existe une application d'un ensemble vide vers un ensemble vide
et donc il existe une application

, cette application est unique et son graphe est
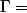
b)Cas de l'ensemble singleton

il n'existe qu'une seule et unique suite

et en fait on vérifie
=e)
c)Cas de l'ensemble non vide et non singleton
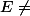
,

Par l'axiome du Choix, le théorême de Zermelo affirme qu'il est possible de munir E d'une relation de bon ordre, celle-ci sera notée

(à ne pas confondre avec celle habituelle dans
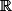
qui elle par contre n'est pas de bon ordre ni d'ailleurs à confondre avec celle de
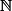
mais comme je dois utiliser encore une autre relation d'ordre les notations sont limitées de fait on se dira que si on parle de E celle ci correspond à cette relation d'ordre là (de bon ordre)
On muni

d'une relation d'équivalence que l'on note

selon

,

alors

si et seulement si
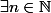
tel que

on vérifie
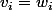
On considère l'ensemble quotient par cette relation d'équivalence que l'on note

qui définit une partition de

selon les classes d'équivalences et on note
_{i\in I})
la famille qui représente cette partition selon
(
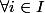
,

) ET (

,

,
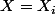
)
on vérifie donc
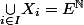
et
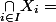
On muni

d'une relation d'ordre partielle que l'on note

telle que:
deux éléments x et y quelconques de

sont comparables par cette relation d'ordre

si et seulement si ils appartiennent à la même classe d'équivalence de

de sorte que

,

,(x

y OU y

x)

(
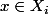
,

,
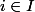
)
Cette relation d'ordre

telle que par cette relation d'ordre,chaque classe d'équivalence constitue un ensemble bien ordonné de sorte que
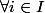
,

,

,

, a est un plus petit élément de

On considère pour chaque élément

la partie que l'on note

telle que

,

alors

,
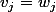
et telle que

,

alors

,

_____________________
on demontre

et en fait
=Card(E))
On considère pour chaque élément

la partie que l'on note

telle que

,

alors

,
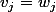
et telle que

,

alors

,

on demontre que

effectivement ici E possède n>1 éléments
on demontre que
=Card(E))
effectivement notons
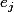
les éléments de E et notons

les éléments de

selon sa construction on obtiens
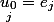
et tous les autres termes des suites de
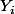
sont identiques
_____________________
on a vu precedemment la partie Y_i d'un X_i et on defini
pour tous

et

alors
 \Leftrightarrow (v0\leq w0))
__________________________________________

,
 \Leftrightarrow (v\underset {\rightarrow}{\leq } w))
__________________________________________
et pour tous

et

alors
on recherche
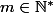
tel que

alors

et

on recherche
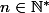
tel que

alors
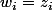
et

avec

n'importe lequel dans Y_i (évident)
n et m existent obligatoirement (évident)
alors lorsque m<n alors
)
et lorsque m=n alors
 \Leftrightarrow (v_m\leq w_n))


