[Défi] Théorème des 7 cercles

[Zweig]

Salut,

Je continue le travail de Timothé :zen: Pour le plaisir de Imod !

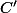
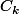
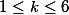
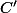
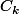
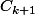
Soit un cercle et 6 cercles , tangents intérieurement à et tels que soit tangent extérieurement à , pour tout .
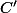
On note , , , , et leur point de tangence avec (voir figure).

Montrer que les droites , et sont concourantes.

[Timothé Lefebvre]

Yop ;)

Ca ressemble à une OIM oui !

[Ericovitchi]

J'ai trouvé un chouette théorème qui pourrait aider :

théorème de Descartes :
Si 4 cercles sont tangents, leur courbure (la courbure c'est +-1/R positive si la tangence est à l'extérieur du cercle, négative sinon.)
sont telles que :
(K1+K2+K3+K4)²=2(K1²+K2²+K3²+K4²)

[oscar]

Bonsoir

On demande une démonstration complète !

[Ericovitchi]

Ben voui mais j'ai cherché et je n'ai pas trouvé grand chose. L'inversion ça n'a pas l'air super probant.

Là je sèche. Si quelqu'un a une démonstration je suis vraiment preneur car ça m'intrigue vraiment ce problème.

[Zweig]

Salut,

J'ai une démo utilisant une inversion de pôle A, donc niveau lycée a priori (bien que ce ne soit pas officiellement au programme, je pense que les profs en font allusion au détour d'un DM en T°S sur le chapitre des complexes, enfin, c'était mon cas en tout cas).

C'était donc bien une piste concluante. :we: Je te laisse continuer sur cette voie, je posterai ma démo demain soir ou après-demain s'il n'y a toujours rien.

[jeremyjeff]

La démonstration complète du théorème des 7 cercles (ainsi que quelques rappels sur l'inversion) est disponible sur le site Math Web: http://www.mathwebs.com

Voici l'url où la trouver:

http://jellevy.yellis.net/Classes/terminale/complexes/Exercices/exo2_inversion_theoreme_sept_cercles.htm

C'est effectivement abordable en classe de terminlae S.

JeremyJeff
A+