Taille de l'image d'un polynôme modulo p.

[Doraki]

Bonjour,

comment vous feriez pour montrer que si f(x) = x^3+x et p est un nombre premier différent de 3, alors { f(x) ; pour x dans Z/pZ } est de cardinal (2p+-1)/3 ? (on choisit le signe pour avoir un entier après la division par 3)

[Ben314]

Dans le cas où p est congru à 1 modulo 3 (<=> -3 est un carré modulo p), j'y arrive... péniblement...
Je regarderais l'autre cas demain

[ffback]

Idem que Ben:
Regardant les "classes d'injectivités":
si ,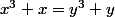
un petit calcul montre que la classe de x a soit 3 soit 1 éléments, selon que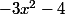 soit un carré ou non, et on se ramene ainsi á regarder l'équation de Pell-Fermat 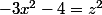. J'obtiens alors que le cardinal cherché vaut oú k est le nombre de solutions de l'équation de Pell-Fermat.

Si -3 est un carré, j'obtiens que k=p-1 ce qui donne le resutat.
Je ne me suis pas encore penché sur l'autre cas

[Ben314]

Sauf erreur, si 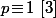le polynôme admet une racine double lorsque 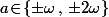où est une des racine carrée de .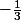
- Donc les classes (pour la relation dont tu parle) de ces quatre là ne contiennent que 2 éléments => 2 classes.
Pour les autres valeurs de , les classes contiennent 1 ou 3 éléments.
- Elle en contiennent 3 ssi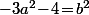 pour un certain 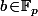dont les solutions peuvent se paramétrer par avec 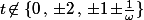soit 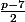tels ( et 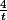donnent la même image) => 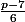classes.
- Il reste éléments dont les classes contiennent un élément => 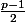classes.
Total :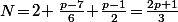 classes.

Si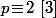 je procède plus ou moins de même :
Les classes contiennent toutes 1 ou 3 éléments
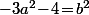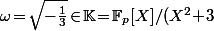- Elle en contiennent 3 ssi pour un certain dont les solutions peuvent se paramétrer par et où et .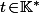
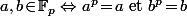qui, sauf erreur, équivaut à qui admet 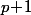solution dans .
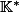Comme et 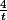donne le même (et que car sinon 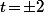qui ne vérifie pas ) il y a 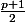dont la classe contient 3 éléments => 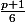classes.
- Il reste éléments dont les classes contiennent un élément => 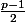classes.
Total : classes.

[ffback]

J'ai effectivement oublié de tenir compte de certaines multiplicités...plusieurs fois...(ce qui au final s'est compensé et a donné le bon résultat!)

[Doraki]

Hmm en effet ça se fait mais c'est assez lourd (l'autre nuit j'arrivais pas à dormir et je me suis demandé si y'avait une sorte de théorème de Cebotarev pour ce genre de truc)

Pour des généralisations, ben vous pouvez essayer x^4+x^3+1, qui si je me gourre pas donne du (15p/24 +O(1)) donc normalement encore un truc affine par morceaux, mais c'est plus compliqué et après c'est plus possible de garder du O(1).

Sinon il y a (x^3+x)/(x-1) mais là c'est plus du O(1) mais du O(sqrt(p)) donc tout de suite c'est moins joli.