Système à 2 équations et 2 inconnues
Olympiades mathématiques, énigmes et défis
-
Koenig
- Messages: 2
- Enregistré le: 03 Oct 2018, 23:55
-
par Koenig » 06 Nov 2018, 22:30
Bonsoir,
Je voudrais trouver l'ensemble des couples x et y réels qui vérifient les 2 équations suivantes :
}}sin(y.ln(k))=0<br />\\\sum_{k=1}^{+\infty}{e^{-x.ln(k)}}cos(y.ln(k))=0<br />\end{matrix}\right.)
Je suis en école d'ingénieur, j'ai actuellement un niveau Bac +3 mais la je ne sais absolument pas comment m'y prendre.
Peut être en transformant l'exponentielle, le sinus et le cosinus en série entière?
Mais bon résoudre une somme infini de polynômes infini, ça m'a l'air un petit peu compliqué...
Modifié en dernier par
Koenig le 06 Nov 2018, 22:42, modifié 2 fois.
-
mathelot
par mathelot » 06 Nov 2018, 22:34
bonsoir,
pour avoir une équation, il faudrait des égalités
-
Koenig
- Messages: 2
- Enregistré le: 03 Oct 2018, 23:55
-
par Koenig » 06 Nov 2018, 22:38
mathelot a écrit:bonsoir,
pour avoir une équation, il faudrait des égalités
Oui désolé petite erreur, j'ai modifié.
-
mathelot
par mathelot » 06 Nov 2018, 22:46
du systeme on en déduit, pour x>1
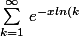}e^{-iy ln(k)}=0)
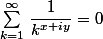
en posant s=x+iy
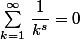
=0)
pour
>1)
or la fonction
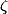
de Riemann ne s'annule pas dans le demi plan
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
