Système de deux triangles

[fatal_error]

slt,

si jdis po de betises : on a comme conditions depuis l'énoncé :
- E,O,B alignés donc il existe k tel que EO = k EB
- E appartient à [FD] donc il existe a tel que FE = a FD
- B appartient à [CA] donc il existe b tel que CB = b CA
- FE/FD = CB/CA donc b = a
on a donc à trouver E, B, a et k à partir des eq du systeme
(1) E,O,B alignés donc il existe k tel que EO = k EB
(2) E appartient à [FD] donc il existe a tel que FE = a FD
(3) B appartient à [CA] donc il existe b tel que CB = a CA

de (2) on exprime E en fonction de a :
E = aFD+F
où E est un point du plan (donc deux coordonnées), idem pour F.

de (3) on exprime B en fonction de a :
B = aCA+C

il reste donc à déterminer a et k à partir de (1) :
on remarque que a et k doivent vérifier EO = kEB pour lequation sur la coordonnée en x ET en y donc on égalise :
x(EO)/x(EB) = y(EO)/y(EB)
Or x(E) = ax(FD)+x(F)
y(E)=ay(FD)+y(F)
x(B)=ax(CA)+x(C)
y(B)=ay(CA)+y(C)
bref l'égalité ne présente que des termes en a.

On a donc une eq du second degré à résoudre en a :
[ xO - xE][yB - yE] = [yO - yE][xB - xE]
j'marrête là, mais ya (normalement) plus qu'à isoler a

[Lostounet]

Ça fait plusieurs heures que j'essaye de passer par de la trigonométrie (comme on a tous les angles, on peut peut-être exprimer les rapports en fonction des angles et isoler), mais j'ai pas réussi... :marteau:

Fatal ! Merci...! Je vais regarder ta méthode de plus près.
Mais il n'y a pas de méthode sans coordonnées? :p

[fatal_error]

voila un ptit script pour tester l'alignement :
Creer fichier.html copier coller le code suivant dedans et ouvrir le fichier avec ff (devrait marcher sous chrome aussi jpense).

Code: Tout sélectionner





#canvas{
  width:500px;
  height:500px;
  background-color:#eeeeee;
}



function plotVect(A,B,ctx){
   ctx.beginPath();
   ctx.strokeStyle='000000';
   ctx.moveTo(A.x, A.y);
   ctx.lineTo(B.x, B.y);
   ctx.closePath();
   ctx.stroke();
}
function plotPoint(A,ctx){
   ctx.fillStyle = '#FF1C0A';
   ctx.strokeStyle='000000';
   ctx.beginPath();
   ctx.arc(A.x, A.y, 2, 0, Math.PI*2, true);
   ctx.closePath();
   ctx.fill();
   ctx.stroke();
}
function Point(ax,ay){
   this.x = ax;
   this.y = ay;
}
function solve(F,D,C,A,O){
   var a = 0;
   var r1 = D.x - F.x,
      r2 = D.y - F.y,
      s1 = A.x - C.x,
      s2 = A.y - C.y;
   
   var bl = s2*O.x - r2*O.x - r1*C.y - F.x*s2,
      al = -r1*s2,
      cl = O.x*C.y - O.x*F.y - F.x*C.y;
   var br = s1*O.y - O.y*r1 - r2*C.x - F.y*s1,
      ar = -r2*s1,
      cr = O.y*C.x-O.y*F.x - F.y*C.x;
   var bs = bl - br;
      as = al - ar;
      cs = cl - cr;
   var sqrtDelta = Math.sqrt(bs*bs-4*as*cs);
   return [(-bs - sqrtDelta)/(2*as), (-bs + sqrtDelta)/(2*as)];
 
}
window.onload=function(){
    var canvas = document.getElementById('canvas');
   var ctx = canvas.getContext('2d');
   var D = new Point(20,2),
      F = new Point(10,100),
      C = new Point(100,100),
      A = new Point(60,3),
      O = new Point(40,50);

   plotVect(F,D, ctx);
   plotVect(C,A, ctx);
   plotPoint(F, ctx);
   plotPoint(D, ctx);
   plotPoint(C, ctx);
   plotPoint(A, ctx);
   plotPoint(O, ctx);
 
 
   var a = solve(F,D,C,A,O);
   var as = a[0];
   if(a[1]>0 && a[1]










Les param a modifier sont les points

Code: Tout sélectionner

var D = new Point(20,2),
      F = new Point(10,100),
      C = new Point(100,100),
      A = new Point(60,3),
      O = new Point(40,50);

[SphinxDeLOblast]

L'égalitée CB / CA = FE / FD n'est pas necessaire pour résoudre ce problème
On peut résoudre indépendamment CB puis en utilisant la même méthode résoudre FE
En fait il faut utiliser le théorême de Heron d'Alexandrie Ier siecle qui stipule :
Si a,b,c sont les trois cotés d'un triangle quelconque alors

est la hauteur de ce triangle en considérant sa base de longueur i et qui est l'un des trois cotés a,b, ou c
avec
En recherchant BC ou AB on applique ce theorême en considérant que la base i = d(OB) désigne celle des triangles OAB et OBC
par ailleurs on pose l'inconnue on obtiens d(CB) = k d(CA)
est la seule inconnue à déterminer

[Dlzlogic]

Bonjour SphinxDeLOblast,
Là, j'ai rien compris.
Il n'est pas possible de calculer indépendamment CB er EF, puisque justement ces deux dimensions sont liées par le fait que EOB sont alignés.

[SphinxDeLOblast]

Bonjour SphinxDeLOblast,
Là, j'ai rien compris.
Il n'est pas possible de calculer indépendamment CB er EF, puisque justement ces deux dimensions sont liées par le fait que EOB sont alignés.

Salut Dlzlogic
Méa culpa ce que tu dit est vrai
j'ai été trompé par la simplicité de l'énoncé
il en résulte pas moins que ce théorême est utile ici

Mille excuses

[Dlzlogic]

Salut Dlzlogic
Utilise ce théorême en prenant la base que j'indique il n'y a rien à comprendre en fait
Certes il est vrai qu'ensuite tu n'est pas obligé d'utiliser la même méthode tu n'a plus qu'à utiliser l'inconnue k que tu as préalablement déterminée

Voyons le problème autrement.
On a une hypothèse parfaitement claire et sans aucune ambiguïté.
J'ai trouvé et décrit une méthode pour déterminer les coordonnées de B et de E
Je crois qu'on ne peut pas trouver une méthode strictement analytique, cad tq XE=, YE, etc.
Ce ne sont pas des pistes de recherche qu'il faut donner, mais un autre solution, si elle existe.

[SphinxDeLOblast]

Salut Dlzlogic
MEA CULPA
Ce que tu dit est vrai
j'ai été bêtement trompé par la simplicité de l'énoncé
Ce que j'ai dit est completement absurde car on ne dispose d'aucune donnée concernant ce point B
autre que le rapport mentionné
Il en résulte pas moins que ce théorême est utile ici

Mille excuses
Je chercherai une solution en l'utilisant

[fatal_error]

Je crois qu'on ne peut pas trouver une méthode strictement analytique

ben c'est un peu ce que j'ai fait...

voir la methode solve, qui n'est que limplem de la resolution de leq [ xO - xE][yB - yE] = [yO - yE][xB - xE] d'inconnue a.

[Dlzlogic]

ben c'est un peu ce que j'ai fait...

voir la methode solve, qui n'est que limplem de la resolution de leq [ xO - xE][yB - yE] = [yO - yE][xB - xE] d'inconnue a.

Oui, quand j'ai écrit cela, je le croyais effectivement.
J'ai bien vu ton graphique, et tout le reste, mais je suis nul en JavaScript je ne sais même plus comment on fait une impression, type impression de contrôle.
Je voudrais l'exécuter avec mes valeurs de test.

[Dlzlogic]

J'ai réussi, et ça marche.

[Doraki]

Si on appelle k le réel tel que CB = k*CA et FE = k*FD (en vecteurs),
alors O,E,B sont alignés
<=> OE^OB =0
<=> (OF+k*FD)^(OC+k*CA)=0
<=> OF^OC + k*(FD^OC+OF^CA) + k²*(FD^CA) = 0

où (v1^v2) = le déterminant de la matrice 2*2 dont les colonnes sont les coordonnées de v1 et de v2 (il faut pas se gourrer dans l'ordre)

Donc il suffit juste de calculer tous ces déterminants et de résoudre une équation de degré 2 pour trouver les k susceptibles de marcher.

[SphinxDeLOblast]

Cette fois-ci ça y est je l'ai (et encore une fois méa culpa pour les bêtises que j'ai précédemment dites)
Pas besoin d'utiliser des vecteurs
J'utilise quand même le théorême de Héron d'Alexandrie du Ier siecle qui stipule :
Si a,b,c sont les trois cotés d'un triangle quelconque alors

est la hauteur de ce triangle en considérant sa base de longueur i et qui est l'un des trois cotés a,b, ou c
avec
Résolution :
Tout d'abord je pose l'inconnue il en résulte que j'obtiens quatre égalités :
d(BC) = k.d(AC)
d(AB) = (1-k).d(AC)
d(EF) = k.d(DF)
d(ED) = (1-k).d(DF)

Ensuite je considere :

la hauteur du triangle definit par les points O,A,B et que je note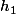 et en considerant que le segment OB constitue la base de ce triangle
la hauteur du triangle definit par les points O,B,C et que je note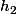 et en considerant que le segment OB constitue la base de ce triangle
la hauteur du triangle definit par les points O,D,E et que je note et en considerant que le segment OE constitue la base de ce triangle
la hauteur du triangle definit par les points O,E,F et que je note et en considerant que le segment OE constitue la base de ce triangle

De sorte que je peut constituer les quatre équations suivantes :






avec quatre les valeurs :






On remplace sur les quatre équations les distances inconnues sur les six car il manque d(OB) et d(OE) selon les quatre équations déjà citées au début:
d(BC) = k.d(AC)
d(AB) = (1-k).d(AC)
d(EF) = k.d(DF)
d(ED) = (1-k).d(DF)

On obtiens donc les quatres équations :







Par ailleurs on peut établir aussi l'égalitée :



On obtiens donc :




Le systeme d'équation obtenue







Permet de résoudre l'inconnue k et les deux distances d(OB) et d(OE) par la même occasion et au final obtenir ce que l'on recherche en appliquant:

d(BC) = k.d(AC)
d(AB) = (1-k).d(AC)
d(EF) = k.d(DF)
d(ED) = (1-k).d(DF)

[Dlzlogic]

Bravo, mais pour l'application numérique, je préfère encore l'itération par dichotomie.
Les ordinateurs n'aiment pas beaucoup calculer des racines carrées tant que ce n'est pas indispensable.

[SphinxDeLOblast]

Bravo, mais pour l'application numérique, je préfère encore l'itération par dichotomie.
Les ordinateurs n'aiment pas beaucoup calculer des racines carrées tant que ce n'est pas indispensable.

mais c'etait oublier Heron (Ier siecle)
et là l'ordinateur et les machines ne servent à rien :ptdr:

[Dlzlogic]

mais c'etait oublier Heron (Ier siecle)
et là l'ordinateur et les machines ne servent à rien :ptdr:

Je suis toujours en admiration pour ces mathématiciens de l'antiquité qui ont presque tout inventé dans ce domaine avec très peu de moyens.
Je pense par exemple aux calculs des dimensions de la terre, rayon et aplatissement, qu'ils ont calculé avec une précision remarquable, je pense aussi à des réalisations architecturales comme le Pont du Gard qui est une prouesse technique de précision, et on ne sait pas comment les romains y sont arrivé.

Concernant le problème précis de Caesar, il s'agit de calcul d'interpolation bilinéaire. Cette méthode de calcul est basée sur une hypothèse précise, et jamais vérifiée. Avec les mêmes données, on peut faire une autre hypothèse, qui dans certains cas est plus probable, que ce quadrilatère se rapproche de l'assemblage de deux triangles accolés par un côté, chaque triangle déterminant un plan, l'interpolation sera faite suivant ce plan. On peut diviser un quadrilatère de deux façons différentes.
Dans d'autres environnements, c'est cette méthode qui est utilisée.

La solution de Fatal_error me parait la plus simple à comprendre, et je vais faire des tests de rapidité.

A ce propos, j'ai testé l'opération 3./7., avec JavaScript. Effectivement la comparaison est bonne. Je n'ai pas d'autre explication que c'est calculé en mode interprété, donc les valeur n'ont pas d'image en mémoire. Ce n'est qu'une interprétation personnelle.

Je vais aussi essayer de comprendre la méthode de Doraki.

[Doraki]

Cette fois-ci ça y est je l'ai (et encore une fois méa culpa pour les bêtises que j'ai précédemment dites)
Pas besoin d'utiliser des vecteurs[...]
Le systeme d'équation obtenu







Permet de résoudre l'inconnue k et les deux distances d(OB) et d(OE) par la même occasion et au final obtenir ce que l'on recherche en appliquant:

d(BC) = k.d(AC)
d(AB) = (1-k).d(AC)
d(EF) = k.d(DF)
d(ED) = (1-k).d(DF)

Non tu as 6 équations et 7 inconnues (k,h1,h2,h1',h2',d(OB),d(OE)).
Ton système permet par exemple de calculer d(OB) et d(OE) en fonction de k, mais il ne te donne pas ce que tu attends.
D'autre part tu n'as jamais utilisé le fait que E,O et B devaient être alignés donc ta démarche ne peut pas être complète.

[SphinxDeLOblast]

Non tu as 6 équations et 7 inconnues (k,h1,h2,h1',h2',d(OB),d(OE)).
Ton système permet par exemple de calculer d(OB) et d(OE) en fonction de k, mais il ne te donne pas ce que tu attends.
D'autre part tu n'as jamais utilisé le fait que E,O et B devaient être alignés donc ta démarche ne peut pas être complète.

Oui effectivement cet alignement doit correspondre à la septieme equation manquante celle_ci



J'utilise la notation pour parler du vecteur OE

Je reviendrai plus tard pour resoudre ce probleme

Donc contrairement à ce que j'ai declaré une premiere fois : il faut utiliser le rapport
puis il faut utiliser le fait que O E B sont trois point appartenants à une même droite

pour l'instant je dispose de sept equations









@+ je reviendrai pour terminer car j'ai trop dit de bêtises
rappel:
1)ON a besoin du rapport
2)Et la propriete d'alignement des points O E B
2)On a besoin de l'utilisation de vecteurs

[Caesar]

Personnellement, la solution de fatal_error me convient parfaitement !
Et en prime le script est fourni, que demander de plus ! Merci beaucoup !

Juste deux petites choses : je ne comprend pas bien à quoi sert le var a = 0; de la première ligne de la fonction solve(F,D,C,A,O), et peut-être as-tu voulu mettre une virgule au lieu d'un point virgule après la déclaration de bs et as ?

[fatal_error]

nan var = 0; sert a rien, dans l'idee jcomptais retourner a, le coeff d'ou l'initialisation puis finalement jretourne directement les deux solutions [-b-sqrtDelta...; -b+sqrtDelta...] a la volee. Bref var a=0; est a supprimer!

edit: et oui, tu as tres bien spotte la virgule au lieu du point virgule. Donc oui il faut mettre soit des virgule, soit des var bs = ...;
(specificite du langage, on peut ne pas specifier var mais ca cree dse variables globales, c'est pas bien :marteau: )