Suites géométriques

[M@thIsTheBest]

Bonjour,
Voilà l'énoncé:
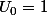
Soit: *la suite définie sur par et
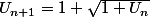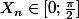
* le réel tel que
Montrer que est une suite géométrique de raison
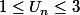
(on peut remarquer que et qu'il existe un unique réel vérifiant cette égalité..)

[chan79]

Bonjour,
Voilà l'énoncé:
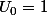
Soit: *la suite définie sur par et
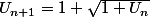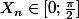
* le réel tel que
Montrer que est une suite géométrique de raison
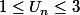
(on peut remarquer que et qu'il existe un unique réel vérifiant cette égalité..)

salut
cos(X(n+1))=
donc
cos²(X(n+1))=
2cos²(X(n+1))-1=
cos(2X(n+1))=cos(X(n))
comme les Xi sont dans [0,pi/2]
2X(n+1)=X(n)
X(n+1) = 1/2 X(n)

Vérif avec geogebra
[img][IMG]http://img228.imageshack.us/img228/1781/sqaz.png[/img][/IMG]