Suite
Olympiades mathématiques, énigmes et défis
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 25 Juin 2007, 11:49
par mt2sr » 25 Juin 2007, 11:49
bonjour
soit
)
une suite croissante positive
Montrer que:
)
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 25 Juin 2007, 11:53
par emdro » 25 Juin 2007, 11:53
Hello,
Qu'as-tu fait?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 25 Juin 2007, 12:31
par mt2sr » 25 Juin 2007, 12:31
de quoi vous parlez
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 25 Juin 2007, 12:46
par emdro » 25 Juin 2007, 12:46
???
De cet exercice que tu nous soumets!
Tu as cherché? Dans quelle voie? Ou bloques-tu?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 25 Juin 2007, 12:57
par mt2sr » 25 Juin 2007, 12:57
ah oui
ton encadrement est pas mal j'ai pas pu trouver mieux est-ce que vous avez d'autres idées
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 25 Juin 2007, 13:08
par emdro » 25 Juin 2007, 13:08
mt2sr a écrit:)
une suite croissante positive
Montrer que:
)
Je parlais de ce nouveau problème!
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 25 Juin 2007, 13:23
par lapras » 25 Juin 2007, 13:23
Par récurrence non ?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 27 Juin 2007, 16:08
par mt2sr » 27 Juin 2007, 16:08
j'ai aucune idée
j'ai essai d'appliquer inégalité de moyenne arithmétique geo mais sans succés
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 09 Juil 2007, 20:03
par lapras » 09 Juil 2007, 20:03
salut,
Il faut montrer que 1/a1 + 2/(a1 + a2) + ... + n/(a1 + a2 + ... + an) < 4 (1/a1 + 1/a2 + ... + 1/an)
ceci équivaut à :
1/2a1 + 2/2(a1 + a2) + ... + n/2(a1 + a2 + ... + an) < 2/a1 + 2/a2 + ... + 2/an
comparons membre a membre :
comme on sait que an est une suite croissante positive, alors 1/(2a1) < 2/a1 ; 2/a2 < 2/(2(a1 + a2)) car 2(a1 + a2)) > a2 car a1 + a2 > a2... tu continues jusqu'au rang n, et tu prouves que l'inégalité.
je suis pas sur...
-
fryters
- Messages: 3
- Enregistré le: 09 Juil 2007, 19:07
-
 par fryters » 12 Juil 2007, 15:06
par fryters » 12 Juil 2007, 15:06
vas déjà jusqu'au rang 5 tu vas voir
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 28 Juil 2007, 17:03
par Imod » 28 Juil 2007, 17:03
Une idée à vérifer ( les calculs sont un peu laborieux !!! ).
D'après l'inégalité de Cauchy-Schwarz , pour

:
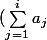(\sum_{j=1}^i \frac{j^2}{a_j})\geq(\sum_{j=1}^ij)^2\geq\frac{i^2(i+1)^2}{4}})
.
Donc pour
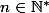
:
^2}(\sum_{j=1}^i \frac{j^2}{a_j})\leq\sum_{i=1}^n\frac{b_i}{a_i}})
.
Avec
^2}<i^2.\sum_{j=i}^{\infty}\frac{1}{j(j+1)^2}})
.
Or
^2}=\frac{1}{j}-\frac{1}{j+1}-\frac{1}{(j+1)^2}})
.
Alors :
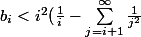<i-i^2\int_{i+1}^\infty \frac{dx}{x^2}\leq i - \frac{i^2}{i+1}\leq\frac{i}{i+1}\leq 1})
.
On a le résultat demandé mais on n'a pas utilisé le fait que

est croissante ce qui est surprenant pour ce type d'exercice !
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 28 Juil 2007, 23:02
par lapras » 28 Juil 2007, 23:02
Bonsoir,
j'ai peut etre trouvé plus simple ^^
Par exemple au rang 3 :
3/2(a1 + a2 + a3) est inférieur à 3/2*3a3 puisque ai est croissante donc 3/(a1 + a2 + a3) est inférieur à 1/2a3 est inférieur à 2/a3 et on généralise au rang n :
n/2(a1+...+an) < n/(2*n*an) < 1/2an < 2/an
membre a membre l'inégalité est vérifiée
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 28 Juil 2007, 23:18
par Imod » 28 Juil 2007, 23:18
Je ne comprends pas tes expressions 3/2*3a3 ? 3/2(a1+a2+a3) ?
Utilises-tu les règles de priorité ou des conventions personnelles ?
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 28 Juil 2007, 23:28
par lapras » 28 Juil 2007, 23:28
Je ne comprends pas tes expressions 3/2*3a3 ? 3/2(a1+a2+a3) ?
j'ai divisé par deux 4(1/a1 + ... + 1/an) et ca équivaut a prouver que :
1/2a1 + 2/2(a1+a2) + ... + n/2(a1+...+an) 3a1 puisque ai est croissante donc a1 + ... + an > n * a1 donc n/2(a1 + ... + an) 2/a1 > 1/2*a1
preuve au rang 4 par ex :
4/2(a1 + ... a4) 2/a1 > 1/2a1
Voila, en fait je m'étais embrouillé dans mon dernier post
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 29 Juil 2007, 02:20
par Imod » 29 Juil 2007, 02:20
lapras a écrit:2/an > 2/a1 > 1/2*a1
Tu en es sûr ?
Imod
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 29 Juil 2007, 09:53
par alben » 29 Juil 2007, 09:53
Imod a écrit:On a le résultat demandé mais on n'a pas utilisé le fait que

est croissante ce qui est surprenant pour ce type d'exercice !
Ce n'est pas étonnant,si on pose :
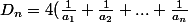-[\frac{1}{a_1}+\frac{2}{a_1+a_2}+...+\frac{n}{a_1+...+a_n}])
on a immédiatement
(4a_2-a_n)...(3a_n)}{a_n(a_1+..a_n)})
Cette quantité est positive si la suite est décroissante ou constante (on n'a plus besoin du facteur 4). Autrement dit, la condition a_n croissant correspond au cas le plus défavorable, où l'inégalité est plus difficile à établir
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Juil 2007, 11:15
par lapras » 29 Juil 2007, 11:15
Imod >
dsl j'ai inversé l'inégalité !
En fait mon résultat devient faux à cause de cette erreur...
Dommage, je pensais que la comparaison membre a membre donnerait du résultat.
alben > comment peut etre sur que 4a1 - an > 0 ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 29 Juil 2007, 11:25
par alben » 29 Juil 2007, 11:25
lapras a écrit:Imod >
alben > comment peut etre sur que 4a1 - an > 0 ?
ce n'est vrai que si la suite est décroissante ou constante
Je voulais simplement répondre à l'interrogation d'Imod (je n'ai pas regardé vos calculs respectifs).
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Juil 2007, 11:51
par lapras » 29 Juil 2007, 11:51
Ok je vois.
Mais en fait la suite est ici croissante.
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 01 Aoû 2007, 15:50
par J-R » 01 Aoû 2007, 15:50
pas mal ce petit exo
a+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
est croissante ce qui est surprenant pour ce type d'exercice !