Suite parfait
Olympiades mathématiques, énigmes et défis
-
karim_2007
- Messages: 7
- Enregistré le: 13 Nov 2007, 20:17
-
 par karim_2007 » 14 Nov 2007, 13:29
par karim_2007 » 14 Nov 2007, 13:29
voila un exercice que g l ai trouvé dans un olympide de sc.math/Bac1 :
on propose la suite suivante: Un =1/n (n appartient à IN*-{1})
1)demonter que il existe un pair natural de (p;q) pour que chaque n de IN* s écrit comme ça: n=2^q(2p+1)
2) demontre que pour n de IN*-{1}: An=1+U2+...+Un "n'appartient pas à" IN
c est facile!!!!!!!!!!!malgrés ça vs avez besoin de courage!bonne chance
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Nov 2007, 13:59
par Nightmare » 14 Nov 2007, 13:59
Bonjour
1) C'est trivial en utilisant la décomposition en facteur premier (une puissance de deux et un produit de facteurs premiers impairs)
2) Je n'ai pas compris, il faut démontrer que pour tout n,
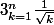
n'est jamais un entier c'est ça?
-
karim_2007
- Messages: 7
- Enregistré le: 13 Nov 2007, 20:17
-
 par karim_2007 » 14 Nov 2007, 20:06
par karim_2007 » 14 Nov 2007, 20:06
:zen: bon, j ai modifier l erreur dans l exercice: il faut demonter que pour n de IN*-{1}: "1+( le ségma de 1/k) " n'apartient po à IN.[ k=(2,3,4,......,n)].merci monsieur bcq pour tes remarques :++:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Nov 2007, 23:15
par ThSQ » 16 Nov 2007, 23:15
Ca doit être un classique celui-là, on l'a étudié l'an dernier.
C'est un récurrence et on montre que c'est impair/pair et donc jamais un entier.
-
karim_2007
- Messages: 7
- Enregistré le: 13 Nov 2007, 20:17
-
 par karim_2007 » 17 Nov 2007, 14:03
par karim_2007 » 17 Nov 2007, 14:03
ok tu peux expliquer ta méthode pour que toout le monde comprend,et merci
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Nov 2007, 21:55
par ThSQ » 17 Nov 2007, 21:55
Prends le k qui a la plus grande puissance de 2 (k = 2^a * (2*b+1), a max) et regarde.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Nov 2007, 22:30
par aviateurpilot » 17 Nov 2007, 22:30
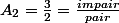
si
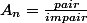
alors
pair}=\frac{impair_1}{pair_1})
c'est bien la reccuence dont
ThSQ a parlé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
