Suite à expliciter

[catamat]

Bonjour

Je cherche à définir cette suite récurrente sous forme explicite, mais je ne sais pas si cela est possible :

Soit k et r deux réels strictement supérieur à 1

Soit la suite telle que =1
et pour tout entier n, on a :


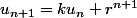
Si vus avez des idées ou des solutions merci d'avance.

[GaBuZoMeu]

Bonjour,

Réponse habituelle : expliciter pour les petites valeurs de n, et voir ce qui se dégage (si quelque chose se dégage).

[mathelot]

bonjour,
écris n égalités;



.....


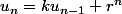
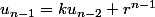
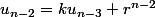
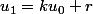
multiplie la deuxième égalité par k
multiplie la troisième égalité par
..
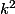
la dernière par

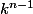
additionne ces n égalités, ça se simplifie et s'écrit comme une somme de n termes
d'une progression géométrique. Une fois trouvé la formule pour , on la démontre par récurrence.

[catamat]

Un grand merci Mathelot....

[mathelot]

bonjour,
écris n égalités;



.....


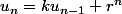
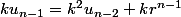
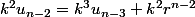
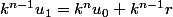
additionne ces n égalités, ça se simplifie et s'écrit comme une somme de n termes
d'une progression géométrique. Une fois trouvé la formule pour , on la démontre par récurrence.

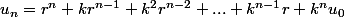
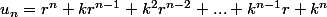
il reste à exprimer cette dernière somme comme la somme des termes en progression géométrique:

à la fin , on trouve

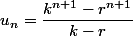
[catamat]

Ok

j'avais pensé à utiliser l'identité remarquable



mais c'est la même chose bien sûr. Encore merci beaucoup