Suite et arithmétique
Olympiades mathématiques, énigmes et défis
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 02 Juin 2012, 13:58
par M@thIsTheBest » 02 Juin 2012, 13:58
Bonjour,
je cherche des exercices difficiles en suite réelles et exercices d'arithmétique dans

niveau première et terminal.
Merci d'avance..
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 02 Juin 2012, 16:10
par M@thIsTheBest » 02 Juin 2012, 16:10
Il n'y a pas de réponses ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Juin 2012, 16:59
par Dinozzo13 » 04 Juin 2012, 16:59
Bonjour, je te propose ça :
Soit
)
une suite arithmétique dont tous les termes sont strictement positifs.
Montrer que :
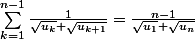
Après c'est sûr que "suite arithmétique", ça restreint pas mal le type d'exo :+++:
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 05 Juin 2012, 13:35
par M@thIsTheBest » 05 Juin 2012, 13:35
Dinozzo13 a écrit:Bonjour, je te propose ça :
Soit
)
une suite arithmétique dont tous les termes sont strictement positifs.
Montrer que :
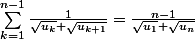
Après c'est sûr que "suite arithmétique", ça restreint pas mal le type d'exo :+++:
Bon voilà ce que j'ai trouvé:
soit P(n):
" 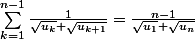

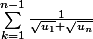 "
"P(2) est vrai (évident), supposant que P(n) est vrai Mq P(n+1) est vrai "

"
On a:
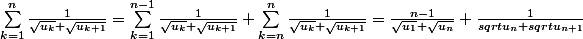
Je pense que je suis sur le point de trouver la solution:je doit utiliser la donnée:

est arithmétique..qu'en pensez vous ?
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 05 Juin 2012, 14:52
par manoa » 05 Juin 2012, 14:52
salut,
essayes avec le conjugué .
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 05 Juin 2012, 21:15
par M@thIsTheBest » 05 Juin 2012, 21:15
manoa a écrit:salut,
essayes avec le conjugué .
Effectivement:l'utilisation du donnée:

est une suite arithmétique et le conjugué :
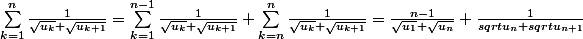
=
(sqrt{u_1}-sqrt{u_n})}{u_1-u_n} + \frac{sqrt{u_n}-sqrt{u_{n+1}}}{u_n-u_{n+1}})
=
(sqrt{u_1}-sqrt{u_n})}{(1-n)r} - \frac{sqrt{u_n}-sqrt{u_{n+1}}}{r})
=
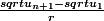
=
r})
=
r})
=
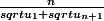
:zen:
Donc d'après le principe de récurrence

n
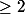
on a
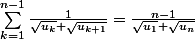
:zen:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juin 2012, 17:39
par Dinozzo13 » 06 Juin 2012, 17:39
Salut !
Ca m'a l'air correct, toutefois, on aurait pu se passer du raisonnement par récurrence :
Comme l'a dit manoa : utilise la quantité conjuguée :
(\sqrt{u_k}-\sqrt{u_{k+1}}) } =\sum_{k=1}^{n-1} \frac{\sqrt{u_k}-\sqrt{u_{k+1}}}{ u_k-u_{k+1} })
.
Or
)
est une suite arithmétique donc il existe un réel

tel que :
pour tout
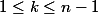
:
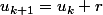
donc

et par suite :
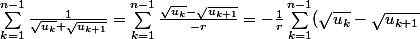)
.
De plus,
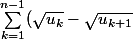= \sqrt{u_1}-\sqrt{u_n})
.
Donc :
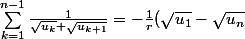= \frac{\sqrt{u_n}-\sqrt{u_1}}{r})
.
On multiplie au numérateur et au dénominateur par la quantité conjuguée et on a :
 } = \frac{n-1}{\sqrt{u_n}+\sqrt{u_1}})
.
:+++:
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 06 Juin 2012, 21:04
par M@thIsTheBest » 06 Juin 2012, 21:04
Bah, c'est ça les mathématiques: différentes démonstrations pour un seul problème..
Merci.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 06 Juin 2012, 21:21
par Zweig » 06 Juin 2012, 21:21
La récurrence n'est pas une chouette technique pour démontrer car elle suppose la connaissance du résultat à l'avance, ce qui n'arrive que dans des cas idylliques (la plupart du temps, scolaires). Elle ne permet rarement de mettre en exergue la "mécanique" sous-jacente au résultat aussi.
La solution de Manoa est plus naturelle je trouve, la tienne est tout aussi valable bien sûr.
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 06 Juin 2012, 21:42
par M@thIsTheBest » 06 Juin 2012, 21:42
Absolument, je suis tout à fait d'accord avec toi.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 07 Juin 2012, 00:26
par Dinozzo13 » 07 Juin 2012, 00:26
Tiens, j'ai eu une petite idée :
Déterminer l'ensemble des suites arithmétiques
)
vérifiant :
a)

;
b)
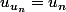
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 07 Juin 2012, 10:47
par M@thIsTheBest » 07 Juin 2012, 10:47
Dinozzo13 a écrit:Tiens, j'ai eu une petite idée :
Déterminer l'ensemble des suites arithmétiques
)
vérifiant :
a)

;
b)
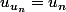
Voilà:
on pose r la raison de la suite et

le 1er terme.
a)


}{2})
=


r)}{2})
=


r))
=


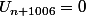
alors je pense que la seule solution est la suite nulle tq
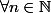
on a
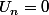
.
b)
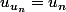

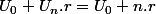

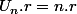
:
si r=0 alors la 1ére solution est la suite constante tq
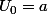
avec
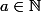
si r

0 alors
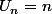
par suite r=1 et
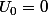
(c'est la deuxième solution.)
Conclusion: il
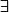
que 2 possibilités vérifiant
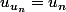
. :zen:
Qu'en pensez vous ?
Et avez-vous svp quelques choses sur les suites géométriques ?
Merci.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 07 Juin 2012, 13:05
par Dinozzo13 » 07 Juin 2012, 13:05
C'est bon :+++:
Tiens, un exo sur les suites géométriques :
Soit (u_n) une suite définie par
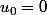
,
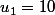
et pour tout entier naturel

:
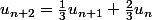
.
On note
)
la suite définie pour tout

par :
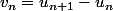
1°)a) Montrer que
)
est géométrique.
b) En déduire
)
en fonction de

.
2°)a) Montrer que
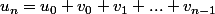
.
b) En déduire
)
.
c)
)
converge-t-elle ?
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 08 Juin 2012, 11:29
par M@thIsTheBest » 08 Juin 2012, 11:29
Dinozzo13 a écrit:C'est bon :+++:
Tiens, un exo sur les suites géométriques :
Soit (u_n) une suite définie par
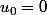
,
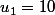
et pour tout entier naturel

:
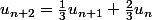
.
On note
)
la suite définie pour tout

par :
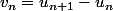
1°)a) Montrer que
)
est géométrique.
b) En déduire
)
en fonction de

.
2°)a) Montrer que
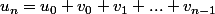
.
b) En déduire
)
.
c)
)
converge-t-elle ?
Bon, voilà :
1°)a et b)
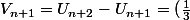U_{n+1} + (\frac{2}{3})U_n - U_{n+1})
=
.V_n)
.
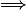

est géométrique de raison q=
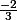
et de premier terme
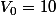
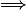
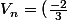^n . 10)
.
2°)a) on a:
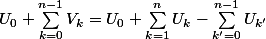
=
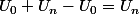
.
b)on a
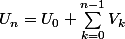
=
.V_n)
=
.V_n)
=
^n])
.
c)
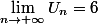
d'ou

converge vers 6. :zen:
Jaimerais tout dabord vous exprimer mes plus sincères remerciements pour les problèmes de suite que tu m'as accordé :+++: , et pourriez vous svp me donner des énoncés d'arithmétiques(divisibilité dans

,nombre premier...
Et merci.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Juin 2012, 14:37
par Zweig » 10 Juin 2012, 14:37
Soit
)
une suite vérifiant :
\in\mathbb{N}^2\,:\|u_m+u_n-u_{n+m}|\leq \frac{1}{m+n})
Montrer que
)
est une suite arithmétique.
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 10 Juin 2012, 15:47
par M@thIsTheBest » 10 Juin 2012, 15:47
Zweig a écrit:Soit
)
une suite vérifiant :
\in\mathbb{N}^2\,:\|u_m+u_n-u_{n+m}|\leq \frac{1}{m+n})
Montrer que
)
est une suite arithmétique.
Je vais mettre une démonstration que j'y réfléchit franchement pour la 1ère fois( si elle est fausse je cherche une autre):
D'après le théorème de gendarme: la limite de la quantité en valeur absolue quant
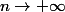
et
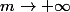
= 0 alors
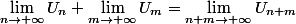
donc la seule possibilité et que U est arithmétique ? Avez vous des contres exemples ?
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 10 Juin 2012, 15:54
par M@thIsTheBest » 10 Juin 2012, 15:54
Zweig a écrit:Soit
)
une suite vérifiant :
\in\mathbb{N}^2\,:\|u_m+u_n-u_{n+m}|\leq \frac{1}{m+n})
Montrer que
)
est une suite arithmétique.
Je vais mettre une démonstration que j'y réfléchit franchement pour la 1ère fois( si elle est fausse je cherche une autre):
D'après le théorème de gendarme: la limite de la quantité en valeur absolue quant
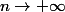
et
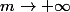
= 0 alors
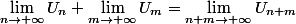
donc la seule possibilité et que U est arithmétique ? Avez vous des contres exemples ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Juin 2012, 15:55
par Zweig » 10 Juin 2012, 15:55
Je ne vois pas en quoi ton égalité est caractéristique d'une suite arithmétique ... L'idée de passage à la limite est correcte, mais elle est mal utilisée ici.
L'idée c'est de montrer que, pour tout naturels n et m :
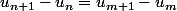
. Pour cela, il serait intéressant de fixer l'une des deux variables (

) et de faire varier l'autre. Néanmoins, l'inégalité telle qu'elle est donnée ici ne suffit pas pour obtenir ce qu'on veut, faut la modifier ...
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 10 Juin 2012, 16:00
par M@thIsTheBest » 10 Juin 2012, 16:00
oui,oui..je l'ai enlevée..
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Juin 2012, 16:02
par Zweig » 10 Juin 2012, 16:02
Si tu pouvais éviter de supprimer tes messages à chaque fois que je te réponds !!!! :mur: Ca fait deux fois déjà
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
une suite arithmétique dont tous les termes sont strictement positifs.
vérifiant :
;
,
et pour tout entier naturel
:
.
la suite définie pour tout
par :
est géométrique.
en fonction de
.
.
.
converge-t-elle ?
une suite vérifiant :
est une suite arithmétique.
une suite vérifiant :
est une suite arithmétique.