Sommes d'entiers consécutifs II
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Nov 2008, 13:19
par Zweig » 22 Nov 2008, 13:19
Salut,
Résoudre dans
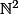
, avec
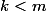
, l'équation suivante :
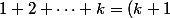 + (k+2) + \cdots + m)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 22 Nov 2008, 13:39
par lapras » 22 Nov 2008, 13:39
Salut,
sans réfléchir,
il suffit de réécrit l'égalité (somme d'une suite arith.)
On tombe sur un polynome de second degré, on calcul delta, qui est lui même un trinome, on re-calcul delta et on conclue.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Nov 2008, 13:56
par Zweig » 22 Nov 2008, 13:56
Sauf erreurs, le

obtenu est fait de telle manière qu'on ne puisse pas déterminer tous les couples
)
tels que
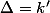
(c'était la première chose que j'avais essayé).
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 22 Nov 2008, 13:59
par guigui51250 » 22 Nov 2008, 13:59
est-ce que la deuxième suite se réécrit (m-k)(k+1+m)??
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 22 Nov 2008, 16:12
par ThSQ » 22 Nov 2008, 16:12
Triplets pythagoriciens, le retour.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
