Somme alternée de Riemann
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Jan 2011, 15:14
par Nightmare » 02 Jan 2011, 15:14
Hello et bonne année à tous !
Problème pour les lycée + :
On sait que pour une fonction continue sur [0,1],
)
converge vers
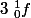
.
Question : Que peut-on dire de
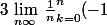^{k}f\(\frac{k}{n}\))
?
:happy3:
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 02 Jan 2011, 17:15
par Matt_01 » 02 Jan 2011, 17:15
Marrant. Pour information, c'est vraiment très court.
-
Anonyme
 par Anonyme » 02 Jan 2011, 17:23
par Anonyme » 02 Jan 2011, 17:23
Salut Nightmare !
Je dirais qu'elle tend vers 0. Déjà c'est assez évident graphiquement si l'on raisonne avec des aires après je pense qu'en revenant a la définition de la continuité on doit arriver a prouver que
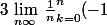^{k}f\(\frac{k}{n}\) < \frac{1}{n} \frac{n\epsilon}{2})
ou quelque chose du genre (si n est impaire) ce qui conclut.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Jan 2011, 18:13
par Nightmare » 02 Jan 2011, 18:13
Oui ça tend bien vers 0. Ce n'est pas seulement à cause de la continuité, mais une notion plus forte ! Laquelle?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Jan 2011, 18:28
par Zweig » 02 Jan 2011, 18:28
L'uniforme continuité.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 02 Jan 2011, 19:27
par benekire2 » 02 Jan 2011, 19:27
Ca nécéssite Heine quand même , on est pas censé savoir ça (mais dans le sens où c'est intuitif...)
:ptdr:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Jan 2011, 19:37
par Nightmare » 02 Jan 2011, 19:37
Une preuve complète?
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 03 Jan 2011, 02:40
par Matt_01 » 03 Jan 2011, 02:40
Je m'en sors sans uniforme continuité pour ma part (mais avec un théorème qui l'utilise, déja cité)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Jan 2011, 14:04
par Nightmare » 03 Jan 2011, 14:04
Matt_01 > ? Peux-tu préciser?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Jan 2011, 21:00
par benekire2 » 03 Jan 2011, 21:00
Matt_01 a écrit:Je m'en sors sans uniforme continuité pour ma part (mais avec un théorème qui l'utilise, déja cité)
Salut !
Si c'est le théorème de Heine, oui c'est l'uniforme continuité , rien de plus :lol3:
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 08 Jan 2011, 15:18
par Matt_01 » 08 Jan 2011, 15:18
Eh bien en utilisant Riemann !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Jan 2011, 13:47
par Nightmare » 09 Jan 2011, 13:47
Comment procèdes-tu Matt ? :happy3:
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 09 Jan 2011, 18:47
par Matt_01 » 09 Jan 2011, 18:47
J'écris la somme de la somme alternée et de la somme non alternée et cela fait apparaitre une somme de Riemann modulo une constante multiplicative.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités