Solution d'un système

[Oliv33]

Bonjour,

Un petit défi : considérons un entier , un réel et une famille de réels définie pour .

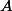
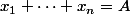
Sous quelles conditions sur et les existe-t-il des réels positifs (ou nuls) tels que et pour tout ?

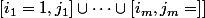
On obtient facilement une condition nécessaire : pour tout recouvrement de , on doit avoir .

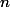
Je pense que c'est aussi suffisant, mais je n'arrive pas à le démontrer pour quelconque. Quelqu'un a une idée ?

Merci !

[Ben314]

Salut,
Ton truc est pas bien clair : tu demande à ce que pour tout mais je vois pas bien à quoi correspond ton .
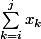
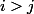
A froid, j'aurais éventuellement conjecturé que ça voulais dire sauf que je vous pas trop à quoi ça pourrait correspondre dans les cas où donc je me demande si c'est pas autre chose...

[Oliv33]

Salut,
Ton truc est pas bien clair : tu demande à ce que pour tout mais je vois pas bien à quoi correspond ton .
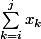
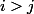
A froid, j'aurais éventuellement conjecturé que ça voulais dire sauf que je vous pas trop à quoi ça pourrait correspondre dans les cas où donc je me demande si c'est pas autre chose...

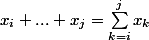
Merci pour la remarque, et désolé pour l'erreur de notation, c'est bien , définie pour seulement.