Un simple pourcentage ? pas si sur ..

[windows7]

salut

on considere la suite Un= 2^n

donnez un devellopement asymtotique du pourcentage des termes de la suite commencants par "1".

Courage :)

[fatal_error]

salut,

ben vu qu'une mult par 2 c'est un shl,
tous les termes de la suite commencent par le chiffre 1.

Mais j'ai du mal comprendre ...

edit, a oublié qu'on compte en base 10 ...

[windows7]

:ptdr: :ptdr: :ptdr:

[Ben314]

Je voterais bien pour (soit environ 30%) mais pour la preuve, ça me parrait assez chaud...

[nodjim]

Je voterais bien pour (soit environ 30%) mais pour la preuve, ça me parrait assez chaud...

Pourquoi cette hésitation ?
dans la suite de 2^n en écriture décimale, il y a autant de 1 de tête que de chiffres, car tout chiffre supplémentaire est 1 en tête, et le 1 n'existe qu'une fois pour un nombre de chiffres donné. Le nombre de "1 en tête" de la suite au rang n est donc le nombre de chiffres du nombre 2^n de la suite.

[windows7]

salut

oui ben c'est bien ca :)
tu donne ta preuve ?

[Doraki]

Bah il vient d'expliquer que pour tout k il existe un unique n tel que 10^k <= 2^n < 2*10^k. (2^n a (k+1) chiffres et commence par 1)

Donc que parmi 2^0,2^1...2^n, comme 2^n a 1+[n*log2/log10] chiffres, il y a exactement 1+[n*log2/log10] exposants k tels que 2^k commence par un 1.

[windows7]

lol doraki je sais que tu sais c'est bon ..

Je lui demande parce qu'il dit que ca lui parait 'assez chaud'

[ffpower]

Je pense qu'il pensait ( tout comme moi ) à utiliser de l'équirépartition modulo 1..J'avoue que je ne pensais pas qu'il y avait une démo élémentaire, c'est assez classe...

edit : est ce que vous savez si c'est possible aussi de récupérer de maniere élémentaire la proportion des 2^n qui commence par 2,3,...,9 ?

[Doraki]

Je note N(n,X) = le nombre d'exposants k entre 0 et n tel que le 1er chiffre de 2^k est dans X.

Avec log2 et log10, on connaît log5, log4 et log8,
ce qui fait qu'on peut espérer obtenir les valeurs exactes de N(n,{1}), N(n,{2,3}), N(n,{4}), N(n,{5,6,7}), N(n,{8,9}).

Et on peut : en notant f(x) = [n*log2/log10], on a :
N(n,{1}) = 1 + f(n)
N(n,{2,3}) = 1 + f(n-1)
N(n,{4}) = n-1-f(n-1)-f(n)-f(n+1)
N(n,{5,6,7}) = 2-n+f(n-2)+f(n-1)+f(n)+f(n+1)
N(n,{8,9}) = n-2-f(n-2)-f(n-1)-f(n)

[Ben314]

Effectivement, pour le coté "assez chaud", j'avais pas réagi que les deux "2" de l'énoncé (celui de 2^n et celui de 10^k=J'était donc effectivement parti sur le problème de l'équirépartition des n.alpha modulo 1 où alpha=ln(2)/ln(10)...

Aprés, il peut être interessant de voir si l'idée de Doraki permet de conclure pour le nombre de 2^n commençant par exemple par 5 ou bien (ce qui est assez similaire) le nombre de 3^n commençant par 1 (pour les 3^n, le cas "trivial" est la répartition de ceux qui commencent par 1 ou 2...)

[kasmath]

salut
qui pourrais nous donner une petite définition de " développement asymptotique du pourcentage des termes de la suite commençants par un terme etc.."

[Ben314]

Pour chaque entier N, tu regarde le nombre 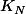d'entiers n entre 1 et N tels que, l'écriture décimale de 2^n commence par un 1 (évidement, 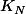est un entier entre 1 et N).
Par exemple : 2,4,8,16,32,64,128,256,512,1024,2048
Ensuite tu regarde la limite (éventuelle) .
Par exemple, si on prend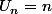 , que peut tu me dire du "développement asymptotique du pourcentage des termes de la suite commençants par un 5" ?
(c'est une vrai question...)

[Ben314]

A propos du problème de départ (plus précisément du cas où on s'y prend mal...) il me semble que, si n'est pas un quotient, alors les restes des modulo 1 (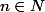) sont équirépartis.
Pour parler (ou plutôt écrire) carré-carré, j'entend par là que :

Sauf erreur, cela découle (aprés quelques encadrements) de la densité des dans [0,1].
Si c'est bien le cas, cela permet d'affirmer directement que, par exemple, la "densité" des puissances de 2 dont l'écriture décimale commence par un 5 est de

[Zweig]

Salut,

Je me disais bien que j'avais déjà vu la généralisation quelque part ... http://moduloserge.free.fr/HX1-05/DM/dm15%28Weyl%29.pdf, dernière page.

[ffpower]

Je suis curieux Ben, comment arrive tu à montrer l'équirépartition à la main? ( bon ça m'étonne pas que c'est possible, la suite des n*lambda étant quand même vachement réguliére )

[Ben314]

Ben... soit je me gourre, soit c'est un peu con-con

On considère un irrationnel et, pour tout 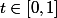on note et, si la limite existe,

Si alors est le nombre de tel que or chaque intervalle contient un unique avec donc .
Comme , cela montre que, si existe alors existe aussi et

Si alors est le nombre de tel que c'est à dire tous sauf les k tels que donc .
Comme , cela montre que, si existe alors existe aussi et

Comme existe et vaut 0 (car est irrationnel) on en déduit que existe et vaut pour tout () et on conclue en utilisant la densité des tels et la croissance des fonctions

[ffpower]

Ok, sympa. J'étais persuadé que l'on pouvait faire sans Weil, et j'étais parti dans cette voie, mais j'avais du mal à bien écrire le truc et à tout faire dans le bon ordre. C'est quand même rassurant de ce dire qu'on est pas obligé de passer par Weil ( et donc du Fourier ) pour montrer ce résultat qui est quand même plutot intuitif^^