Série et suite
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 02 Juin 2012, 14:39
par MMu » 02 Juin 2012, 14:39
Bonjour ami(e)s des maths. Voici un problème que je soumets à votre sagacité.
Soient :
-

une série convergente à termes réels positifs et
-

une suite croissante et non-bornée de réels positifs.
Montrer que la suite
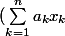/a_n)
converge et calculer sa limite .
:zen:
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 02 Juin 2012, 14:53
par M@thIsTheBest » 02 Juin 2012, 14:53
MMu a écrit:Bonjour ami(e)s des maths. Voici un problème que je soumets à votre sagacité.
Soient :
-

une série convergente à termes réels positifs et
-

une suite croissante et non-bornée de réels positifs.
Montrer que la suite
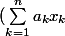/a_n)
converge et calculer sa limite .
:zen:
Cet exercice pour quel niveau, secondaire ou Supérieur ?
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 15:05
par globule rouge » 02 Juin 2012, 15:05
M@thIsTheBest a écrit:Cet exercice pour quel niveau, secondaire ou Supérieur ?
supérieur, cela ne se voit-il pas ?

-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 02 Juin 2012, 15:16
par M@thIsTheBest » 02 Juin 2012, 15:16
globule rouge a écrit:supérieur, cela ne se voit-il pas ?

Je suis encore en secondaire.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 15:19
par globule rouge » 02 Juin 2012, 15:19
M@thIsTheBest a écrit:Je suis encore en secondaire.
Je sais, moi aussi ^^
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 02 Juin 2012, 15:31
par manoa » 02 Juin 2012, 15:31
MMu a écrit:Bonjour ami(e)s des maths. Voici un problème que je soumets à votre sagacité.
Soient :
-

une série convergente à termes réels positifs et
-

une suite croissante et non-bornée de réels positifs.
Montrer que la suite
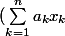/a_n)
converge et calculer sa limite .
:zen:
Salut, je n'ai aucune connaissance en série , je risque donc de dire des bêtises, une tentative :
on note la suite :

on a
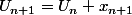
en sommant on trouve
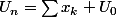
soit l la limite de

alors
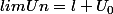
Edit: aie aie j'ai écrit des bêtises ! n'y prêtez pas attention !
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 02 Juin 2012, 16:13
par Le_chat » 02 Juin 2012, 16:13
Salut.
Si on prend n0 un entier, pour n plus grand que n0, en coupant la suite en deux:
un=somme des (ak/an)xk pour n0
Et par croissance de (an):
un;) somme des xk, k>n0+ an0/an somme des xk, k;)n0
Lorsque n tend vers l'infini, le terme de droite tend vers somme des xk, k>n0, et comme cette suite (de la variable n0) tend vers 0, on obtient que (un) tend vers 0. (enfin il faut bien le rédiger mais je pense que ça marche comme ça)
@manoa: ta relation de récurrence entre Un et Un+1 ne marche malheureusement pas.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 02 Juin 2012, 22:51
par Matt_01 » 02 Juin 2012, 22:51
Ouep, pour que ce soit plus clair on peut écrire :
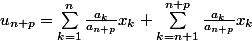
et faire tendre p vers +inf
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
une série convergente à termes réels positifs et
une suite croissante et non-bornée de réels positifs.
converge et calculer sa limite .
une série convergente à termes réels positifs et
une suite croissante et non-bornée de réels positifs.
converge et calculer sa limite .