Etudier la convergence de
Série numérique
7 messages
- Page 1 sur 1
C'est assez tendu, mais on montre que ça converge pour |x|1, on utilise |sin|;)1 et ça montre que ça diverge.
Sinon, on dit que pour un n quelconque, on prend un entier naturel p tel que | |;)
|;) .
.
On a pour ce p, par pi périodicité de |sin|:|sin( )|=|sin(
)|=|sin( )|.
)|.
Comme on est sur [0,pi/2], on utilise |sin(x)|;) |x| pour tomber sur:
|x| pour tomber sur:
|sin( )|;)
)|;)=2n(\sqrt{2}-\frac{p}{n})) .
.
Comme s'approche mal par des rationnels, ça va marcher:
s'approche mal par des rationnels, ça va marcher:
(\sqrt{2}+\frac{p}{n})=2-\frac{p^2}{n^2}=\frac{2n^2-p^2}{n^2})
Et comme n'est jamais nul et que c'est un entier:
n'est jamais nul et que c'est un entier:
|(\sqrt{2}+\frac{p}{n})) |;)
|;)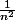 , et:
, et:
) ;)
;)
Donc|sin( )|;)
)|;)
Et la somme converge si |x|<1, diverge si |x|=1.
Sinon, on dit que pour un n quelconque, on prend un entier naturel p tel que |
On a pour ce p, par pi périodicité de |sin|:|sin(
Comme on est sur [0,pi/2], on utilise |sin(x)|;)
|sin(
Comme
Et comme
|
Donc|sin(
Et la somme converge si |x|<1, diverge si |x|=1.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
