Oui, c'est exactement ça (modulo le fait que quand tu parle de "la période des suites Ux définies par..." je pense que tu parle évidement de la suite modulo un polynôme irréductible fixé)
Si tu veut les "étapes manquante" pour en arriver à ces conditions, ce n'est pas super compliqué :
On part d'un rectangle

dont certaines cases sont grisées et on note

les vecteurs colonnes

correspondant aux cases grisées (1=grisé, 0=non grisé).
Dans l'exemple de départ :
\ , \<br />d_2\!=\!\left(\matrix{\!1\!\cr\!0\!\cr\!1\!}\right)\ , \<br />d_3\!=\!\left(\matrix{\!1\!\cr\!1\!\cr\!1\!}\right)\ , \<br />d_4\!=\!\left(\matrix{\!0\!\cr\!0\!\cr\!0\!}\right))
On note aussi

les vecteurs colonnes

correspondant aux centres des croix que l'on va "appliquer" à la grille.
Dans la soluce de départ :
\ , \<br />v_2\!=\!\left(\matrix{\!0\!\cr\!1\!\cr\!0\!}\right)\ , \<br />v_3\!=\!\left(\matrix{\!1\!\cr\!1\!\cr\!0\!}\right)\ , \<br />v_4\!=\!\left(\matrix{\!1\!\cr\!0\!\cr\!0\!}\right))
(5 étapes -> 5 '

')
On constate que l'application des croix transforme la colonne

qui au départ vaut
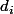
en

où

est la matrice

entièrement nulle sauf sauf sa diagonale et les cases au dessus et en dessous de la diagonale qui contiennent des

(en convenant que

).
On veut rendre tout les

nuls et sela impose de prendre

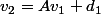
v_1+Ad_1+d_2)
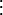
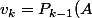v_1+P_{k-2}(A)d_1+P_{k-3}(A)d_2+\cdots+P_1(A)d_{k-2}+P_0(A)d_{k-1})
où la suite de polynômes
_{k\geq 0})
est définie par
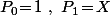
et

Le problème se ramène alors à trouver
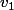
tel que

c'est à dire tel que :
v_1=P_{m-1}(A)d_1+P_{m-2}(A)d_2+ \cdots + P_1(A)d_{m-1}+P_0(A)d_{m})
On en déduit qu'il y a une solution quelque soit la disposition de départ si et seulement si
)
est inversible, c'est à dire si et seulement si
)
est premier avec le polynôme caractéristique de

qui s'avère (aprés un mini calcul) être
)
Par rapport à ta dernière question :
Doraki a écrit:Et est-ce qu'en prime le degré du polynôme minimal donne les dimensions du noyau des morphismes dont on parlait au début ?
Je pense que tu parle du morphisme qui à une matrice nxm (correspondant au centre des croix) associe la matrice nxm des modifications que l'application de ces croix produit. Dans ce cas, il me semble que son noyeau est trés fortement lié à celui de la matrice
)
et je pense que ce dernier est lié à la nature du
,P_n(1-X)\right))
.
Je regarderais bien, dans un cadre trés général, le lien entre le noyeau de P(A) et le pgcd(P,Q) où Q est le polynôme caractéristique de A [peut-être faut il prendre pour Q le polynôme minimal ? dans le cas ou le pgcd=1, cela ne change rien]
P.S. Concernant la suite de polynômes, il semble assez clair (comme tu le suggérais dans ton post concernant l'ensemble A) qu'il vaudrait mieux travailler avec la suite

régie par la même récurence mais d'amorce

.
En plus, dans se cas, si on "inverse" la récurence on a

, qui donne

pour les négatifs
P.S.2 : En fait, pour reprendre ce que tu dit, si
)
est un couple de
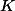
(cloture algébrique de

) et si on prend

tels que

et

alors les ordres n et m de

et

fournissent un des couples de A.
Le problème est de savoir si on peut dire quelque chose de ces ordres ?
Je me demandais s'il ne fallait pas regarder où "vivent" x,y et z (i.e. dans quel

avec

) et voir si on en déduit quelque chose...

