Le Rouge et le Bleu
Olympiades mathématiques, énigmes et défis
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Sep 2008, 18:05
par Imod » 17 Sep 2008, 18:05
Un exercice curieux que je viens de découvrir ( je n'ai pas de solution

)

La figure représente une fonction polynômiale de degré 4 , les tangentes en A et B sont confondues et parallèles à la tangente en C : comparer les aires bleus et rouges :doh:
Bon courage !
Imod
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 18 Sep 2008, 10:53
par scelerat » 18 Sep 2008, 10:53
J'ai formule le probleme dans le repere centre en C, dont la tangente forme l'axe des x, et il me semble deja en deduire x_A = -x_B. On peut donc les mettre egaux a 1 et -1 sans perte de generalite. L'equation de la courbe s'ecrirait alors y = 1/4 (x^4-2x^2).
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 18 Sep 2008, 16:36
par Imod » 18 Sep 2008, 16:36
Avec un raisonnement analogue et un petit calcul intégral j'arrive à

mais tout ça est particulièrement inélégant

.Peut-on faire plus joli ?
Imod
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 19 Sep 2008, 22:45
par Imod » 19 Sep 2008, 22:45
N'ayant pas plus simple pour le moment :zen: . Dans un repère d'origine C dont l'axe des abscisses est parallèle à (AB) et l'unité bien choisie l'équation de la courbe est
=x^4+nx^3+px^2)
.

Comme 0 ,

et

sont les racines de
=x(4x^2+3nx+2p))
,
=-3n)
et
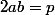
.
L'égalité
=f(b))
se traduit par :
+n(a^3-b^3)+p(a^2-b^2)=0)
C'est à dire :
(a^2+b^2+p)+n(a^2+b^2)+nab=0)
alors
^2=0)
donc

,
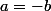
et
=x^4-2b^2x^2)
.

s'annule en

,

et

.
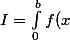dx=-\frac{7b^5}{15}})
,
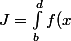dx=-\frac{(7-8\sqrt{2})b^5}{15}})
.
L'aire bleue est égale à

et l'aire rouge

c'est à dire

.
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités


