Bon, je te rerédige la preuve de façon plus détaillée pour voir si cele te va mieux.
On renumérote les nombres du premier disque de façon à avoir 0,1,2,...,n-1 dans cet ordre et évidement, on fait les mêmes changements de numéros sur le second disque.
On a alors :
&f(1)&f(2)&\cdots&f(i)&\cdots&f(n-1)})
où f est une bijection de
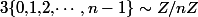
dans lui même.
Lorsque l'on tourne le disque 1 de k secteurs (où
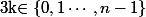
) on a :
&f(1)&f(2)&\cdots&f(i)&\cdots&f(n-1)})
où les nombres de la première ligne sont à prendre modulo n (par exemple
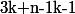
).
Pour une bijection f donnée, la question de l'énoncé se reformule alors sous la forme :
"Existe t'il un k tel que, pour tout i on ait
)
modulo n ?"
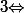
"Existe t'il un k tel que, pour tout i on ait
-i\not\equ k)
modulo n ?"
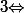
"La fonction
-i)
(modulo n) est-elle non surjective ?"
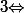
"La fonction
-i)
(modulo n) est-elle non bijective ?"
Car pour une fonction d'un ensemble fini dans lui-même, il y a équivalence entre injective, surjective et bijective.
Arrivé à ce point, on écrit que,
si -i}) (modulo n) est bijective
(modulo n) est bijective on doit avoir :
-i\big)\equ\sum_{k=0}^{n-1}k)
(modulo n)
Or, comme f est bijective, on a
=\sum_{j=0}^{n-1}j)
donc
-i\big)\equ 0)
On doit donc avoir
}{2})
(modulo n) ce qui signifie que

est entier, c'est à dire que n est impair.
On vient de montrer que :
"
-i)
(modulo n) bijective implique n impair"
donc, par contraposition
"n pair implique
-i)
(modulo n) non bijective"
Ce qui signifie que, si n est pair, il y a forcément une solution.
Si n est impair, les deux exemples donnés par Doraki correspondent à :
1)
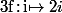
(modulo n) qui est bijective (car n est impair) et
-i=i)
est évidement elle aussi bijective.
2)
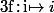
est clairement bijective mais
-i=0)
ne l'est clairement pas.
Ce qui montre uniquement que, si n est impair, la fonction
-i=0)
peut être ou ne pas être bijective, c'est à dire qu'il peut y avoir ou ne pas y avoir de solution.

