Réseau

[MMu]

Soit un ensemble de réels avec la propriété .
Montrer que si est un entier positif pair et alors ..

[Ben314]

Salut,
Si je me suis pas trop gourré, on prend pour l'ordre de 2 dans le groupe multiplicatif ((Z/(m+1)Z)*,x) (inversibles de l'anneau Z/(m+1)Z) voire ou tout autre entier tel que divise .
Ensuite, on regarde l'écriture de en binaire et la séquence des 0 / 1 dans cette écriture donnent mécaniquement une séquence de permettant de passer de à

[Doraki]

J'appelle f et g les deux fonctions
f envoie [0;∞] sur [0;1] et g envoie [0;∞] sur [1;∞] (un peu comme l'algo d'euclide tiens)
Donc en fait c'est nettement plus facile d'aller dans l'autre sens puisqu'on a qu'un seul choix pour remonter (sauf quand on est sur 1 mais après de toutes façons on est coincé sur 0 et ∞)

Si on appelle F(x) = f-1(x) si x <1 ; g-1(x) si x >1,
on peut aller de x à y avec f et g <=> on tombe sur x en itérant F sur y (avec le détail pour 1 qui donne sur 0 ou ∞)

f-1(a/b)= (a-b) /2b et g-1(a/b) = 2a / (b-a)
Donc déjà, la somme numérateur + dénominateur ne change pas (enfin elle peut diminuer si on fait les éventuelles simplifications), donc au bout d'un moment soit on tombe sur 1 soit on tourne en rond.

Mais si en plus a+b = 1 mod 2, alors on ne peut pas tomber sur 1, donc si n est un entier impair et qu'on regarde En = {a/b, a+b=n} alors F y est injective (les images de f-1 et de g-1 sont disjointes il suffit juste de voir qui est pair dans la fraction). Comme En est fini, F est donc une permutation.

comme F(2n/1) = (2n-1)/2, ces deux éléments sont dans la même orbite de F et c'est ce qu'on voulait montrer.


Après avoir lu la réponse de Ben, effectivement, F(a/b) = ((2a) mod (a+b)) / ((2b) mod (a+b)) du coup on voit bien le rôle joué par 2 et son ordre multiplicatif mod (a+b)

[Ben314]

Perso, j'avais procédé "dans le sens direct" ce qui rend le truc plus chiant que ce que fait Doraki vu qu'on a a priori plusieurs possibilités pour les images.
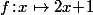
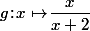
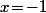
Par contre, là où j'avais fait un peu plus simple, c'est que les deux homographies et ont, comme par hasard, un point fixe commun et que je m'était empressé de conjuguer pour l'envoyer sur histoire d'y voir plus clair :
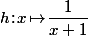
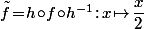
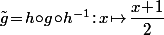
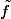
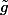
Si alors et et le but est d'envoyer sur à l'aide de et et on trouve assez rapidement comment procéder.

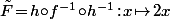
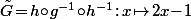
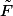
Et le plus simple est évidement de combiner les deux idées en considérant et où le but est d'envoyer sur à l'aide de et .
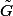
Là, on voit assez clairement comment faire et le lien avec la base 2.

[MMu]

Je vais peut être écrire quelque chose d'équivalent aux solutions de Ben et Doraki .. poursuivons ..
Pour toute fraction positive et irréductible on définit la fonction injective
,
On observe que si , avec irréductibles, alors on a l'invariant .
L'invariance et l'injectivité permettent de dire que pour pair on a un cycle fini
avec l'invariant
Il existe donc tel que
Pour le fun prenons , invariant 20+1=21, et on a le cycle :