Existe t il un nombre N entier de k chiffres (expression décimale), le dernier chiffre n'étant pas zéro, et k aussi grand que l'on veut, de telle sorte que les k derniers chiffres de N² forment ce nombre N ?
Soit un nombre N composé de k chiffres, qui ne sont pas uniquement des 0 ou des 5. Montrer qu'il existe un autre nombre N' de k chiffres, de telle sorte que les k derniers chiffres de N² et N'² forment le même nombre.
Réflexions sur carré
6 messages
- Page 1 sur 1
Pour la question 1, si j'ai bien compris compris ta question se reformule ainsi : Pour k fixé, existe t-il M et N tel que 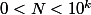 et
et 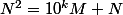 , autrement dit tel que N(N-1) soit multiple de
, autrement dit tel que N(N-1) soit multiple de 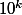 . ( tu rajoutes l'hypothese que N ne finit pas par 0, mais cette hypothese me semble superflue..). Comme N et N-1 sont premiers entre eux, ceci signifie que l'un de ces 2 nombres est multiple de
. ( tu rajoutes l'hypothese que N ne finit pas par 0, mais cette hypothese me semble superflue..). Comme N et N-1 sont premiers entre eux, ceci signifie que l'un de ces 2 nombres est multiple de 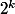 , et qu'un de ces 2 nombres est multiple de
, et qu'un de ces 2 nombres est multiple de 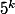 . Comme
. Comme 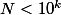 , on doit avoir en fait que l'un des 2 est multiple de
, on doit avoir en fait que l'un des 2 est multiple de 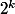 et l'autre de
et l'autre de 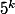 . Traitons par exemple le cas ou N est multiple de
. Traitons par exemple le cas ou N est multiple de 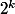 . On doit donc avoir
. On doit donc avoir 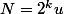 et
et 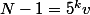 pour un certain (u,v), et donc
pour un certain (u,v), et donc  . Cette équation se résout de maniere classique grace à Bezout, et a une unique solution (u,v) telle que
. Cette équation se résout de maniere classique grace à Bezout, et a une unique solution (u,v) telle que 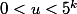 , et donc telle que
, et donc telle que 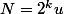 soit plus petit que
soit plus petit que 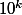 . Il y a donc une unique solution N qui soit multiple de
. Il y a donc une unique solution N qui soit multiple de 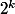 . De la même maniere, il y a une unique solution N multiple de
. De la même maniere, il y a une unique solution N multiple de 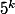 . Au final, à k fixé il y a donc exactement deux N qui conviennent..
. Au final, à k fixé il y a donc exactement deux N qui conviennent..
EDIT: par contre je me rend compte que ma solution ne dit pas si ces solutions N sont "propres", dans le sens ou elles pourraient a priori être plus petites que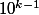
EDIT: par contre je me rend compte que ma solution ne dit pas si ces solutions N sont "propres", dans le sens ou elles pourraient a priori être plus petites que
Pour ce genre de trucs faut se placer dans les complétés n-adique de Q, ça fait plus joli.
l'équation x² = x a 2 solutions dans Z(2) et Z(5), 0 et 1.
Comme Z(10) = Z(2) * Z(5) (bézout),
Ca en fait 4 solutions dans Z(10),
0; 1;
a = ...106619977392256259918212890625.
b = ...893380022607743740081787109376.
(on note que a+b = 1 et a*b = 0)
Pour l'autre question, il s'agit de résoudre x²-n² = 0,
c'est à dire (x-n)(x+n) = 0.
Si n = 0 alors il y a une seule solution (0) dans Z(2) et dans Z(5), donc 1 seule solution (0) dans Z(10).
Sinon, on a 2 solutions différentes dans Z(2) et Z(5) , n et -n, ce qui donne 4 solutions dans Z(10).
Par exemple, si n = 5, ça donne
...00000000005.
...99999999995. (-5)
...17871093755.
...82128906245.
Elles se terminent toutes par 5, mais si n se termine par un autre chiffre que 5 ou 0, on peut immédiatement commencer à différencier des solutions.
l'équation x² = x a 2 solutions dans Z(2) et Z(5), 0 et 1.
Comme Z(10) = Z(2) * Z(5) (bézout),
Ca en fait 4 solutions dans Z(10),
0; 1;
a = ...106619977392256259918212890625.
b = ...893380022607743740081787109376.
(on note que a+b = 1 et a*b = 0)
Pour l'autre question, il s'agit de résoudre x²-n² = 0,
c'est à dire (x-n)(x+n) = 0.
Si n = 0 alors il y a une seule solution (0) dans Z(2) et dans Z(5), donc 1 seule solution (0) dans Z(10).
Sinon, on a 2 solutions différentes dans Z(2) et Z(5) , n et -n, ce qui donne 4 solutions dans Z(10).
Par exemple, si n = 5, ça donne
...00000000005.
...99999999995. (-5)
...17871093755.
...82128906245.
Elles se terminent toutes par 5, mais si n se termine par un autre chiffre que 5 ou 0, on peut immédiatement commencer à différencier des solutions.
Je ne m'y connais pas bien en p-adique ( comprendre par la "pas du tout" ^^)
Je sais juste que ca consiste à regarder les "développements infinis" en base p, qui convergent pour la topologie correspondante. Mais apres :d'ou sors tu ces a et b? Comment reviens tu dans N ensuite?
D'autre part, en faisant quelques essais sur des petits cas, j'ai l'impression que si N est un multiple de 5, alors N est une puissance de 5..Est ce que ta méthode permettrait d'obtenir cette info?( a supposer qu'elle soit vraie )
Je sais juste que ca consiste à regarder les "développements infinis" en base p, qui convergent pour la topologie correspondante. Mais apres :d'ou sors tu ces a et b? Comment reviens tu dans N ensuite?
D'autre part, en faisant quelques essais sur des petits cas, j'ai l'impression que si N est un multiple de 5, alors N est une puissance de 5..Est ce que ta méthode permettrait d'obtenir cette info?( a supposer qu'elle soit vraie )
Ben on revient dans N en coupant où tu veux dans le développement.
Dire que tout ça marche en p-adique ça revient à dire que si tu as une solution de x² = x mod 10^n alors en regardant ces solutions là modulo 10^m avec m <= n, ça te donne immédiatement une solution modulo 10^m.
Donc autant regarder les 4 solutions pour n arbitrairement grand, ça te donne toutes les solutions modulo 10^m pour m <= n.
Les solutions mod 10^m et mod 10^n sont "cohérentes" entre elles.
Après ce qu'est bien c'est que si p est premier, Z(p) est intègre donc on peut factoriser X²-X pour décrire les solutions de X²-X dans Z(p), = les solutions de X²-X dans tous les Z/p^nZ.
Après, bah Z(10) c'est pas intègre mais c'est Z(2) * Z(5) c'est pour ça qu'il faut regarder d'abord dans Z(2) et Z(5)
Je suis pas sûr de ce que tu veux dire pour les multiples/puissances de 5 mais par exemple 90625 * 90625 = 8212890625 mais 90625 n'est pas une puissance de 5 (alors que 0625, 625, 25 et 5, si, je te l'accorde)
Dire que tout ça marche en p-adique ça revient à dire que si tu as une solution de x² = x mod 10^n alors en regardant ces solutions là modulo 10^m avec m <= n, ça te donne immédiatement une solution modulo 10^m.
Donc autant regarder les 4 solutions pour n arbitrairement grand, ça te donne toutes les solutions modulo 10^m pour m <= n.
Les solutions mod 10^m et mod 10^n sont "cohérentes" entre elles.
Après ce qu'est bien c'est que si p est premier, Z(p) est intègre donc on peut factoriser X²-X pour décrire les solutions de X²-X dans Z(p), = les solutions de X²-X dans tous les Z/p^nZ.
Après, bah Z(10) c'est pas intègre mais c'est Z(2) * Z(5) c'est pour ça qu'il faut regarder d'abord dans Z(2) et Z(5)
Je suis pas sûr de ce que tu veux dire pour les multiples/puissances de 5 mais par exemple 90625 * 90625 = 8212890625 mais 90625 n'est pas une puissance de 5 (alors que 0625, 625, 25 et 5, si, je te l'accorde)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
