La forme obtenue est un TORE.
Mais on va faire une grosse impasse... on va considérer que le volume obtenu est un fil d'or. On vérifiera à la fin si cette impasse est acceptable ou pas.
Je note D le diamètre du fil.
La longueur du fil est le périmètre du cercle de diamètre 60mm ; c'est 60*Pi Mais je vais le noter x *Pi ( parce que tu veux pouvoir adapter les calculs à d'autres valeurs de x )
La section du fil est de Pi * (D/2)²
Le volume du fil est de x * Pi * Pi * (D/2)² = x * Pi² * D² / 4
Le poids du fil est de ?
Là, il faut faire attention. Le volume ci-dessus est en millimètres-cubes.
La densité qu'on nous donne est en quelle unité ? 16 Tonnes par metre cube ... c.a.d. 16 kg par décimètre cube, c.a.d. 16 grammes par centimètres cube ou enfin 0.016 grammes par millimètres cube.
Le poids du fil est donc de x * Pi² * D² / 4 * 0.016 grammes , ou x * Pi² * D² * 0.004
Et on veut que ce nombre donne 20 grammes. Pds = 20 dans cet exemple.
Donc on a l'équation : x * Pi² * D² * 0.004 = Pds où l'inconnue, c'est D.
On isole D :
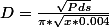
Avec les données de l'exemple ( poids = 20 grammes, Diamètre intérieur = 60 mm), ça donne un diamètre pour le fil de 2.9 mm.
Problème. Comparativement au 60mm du diamètre intérieur, ce 2.9 millimètres n'est pas négligeable.
L'impasse faite n'est pas satisfaisante.
Le poids d'or disponible permet de faire un tore de 60 millimètre de diamètre et avec une section circulaire de 2.9mm, mais ce 60 millimètre n'est pas le diamètre intérieur, c'est le diamètre moyen.
Le diamètre intérieur va être environ 60-2.9= 57.1 ...
Dans les faits, il faut un diamètre d'environ 2.75mm pour ces données.
Voilà déjà une première approche, simplifiée. Peut-être que d'autres seront plus courageux, et donneront une formule plus précise.
) 
et je t'avoue que je suis un peut perdu dans tes calculs 
, il faut que je comprenne pour arriver a faire les calculs dans une feuille excel 
..... c'est pour ca que je fessai la remarque .
