Simplifier ces racines:
Racine carrée (défi de la classe de Seconde)
12 messages
- Page 1 sur 1
racine carrée (défi de la classe de Seconde)
par mathelot » 19 Déc 2018, 13:46
Bonjour,
Simplifier ces racines:
^{2010}+(\sqrt{2}-1)^{-2010}})
 \, \left( \frac{ 2^{2010}+1 }{\sqrt{2}} \right) +1})
(2^{2012}-2^{2011}+2^{2010}-2^{2009})}{3}})
 \left( \frac{1}{2^{2011}}+\frac{1}{2^{2010}}+\frac{1}{2^{2009}} \right)})
\left( \sqrt{1}+\sqrt{2}-\sqrt{3} \right)\left( \sqrt{2}+\sqrt{3}-\sqrt{1} \right)\left( \sqrt{1}+\sqrt{3}-\sqrt{2} \right)})
Simplifier ces racines:
Re: racine carrée (défi de la classe de Seconde)
par FLBP » 19 Déc 2018, 14:46
La première c'est une identité remarquable :
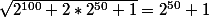
La deuxième aussi:
} = \sqrt{2}(2^{49}-2^{-51}))
La deuxième aussi:
Modifié en dernier par FLBP le 19 Déc 2018, 14:53, modifié 1 fois.
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 19 Déc 2018, 14:53
la 3, un (bon) élève de seconde peut tenter une quantité conjuguée
Re: racine carrée (défi de la classe de Seconde)
par mathelot » 19 Déc 2018, 18:43
pascal16 a écrit:la 3, un (bon) élève de seconde peut tenter une quantité conjuguée
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 19 Déc 2018, 18:44
tu as eu un avis favorable pour passer en première au conseil de classe ?
pour le 2 reconnaître (1/2)*(a-b)², a = 2^50...
pour le 2 reconnaître (1/2)*(a-b)², a = 2^50...
Modifié en dernier par pascal16 le 19 Déc 2018, 18:50, modifié 1 fois.
Re: racine carrée (défi de la classe de Seconde)
par mathelot » 19 Déc 2018, 18:46
pascal16 a écrit:tu as eu un avis favorable pour passer en première au conseil de classe ?
hélas , trop de bavardages..
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 23 Déc 2018, 15:29
la 4 :
3(√2+1)^2010+1/(√2-1)^2010
= [3(√2+1)^2010(√2-1)^2010 +1 ] / D
= [3((√2+1)(√2-1))^2010 +1 ] /D
= [3(1)^2010 +1 ] /D
= 4/D
donc (4)= 2/((√2-1)^1005)=2*(√2+1)^1005
peut se mettre sous la forme a+b√2, y a un autre cheminement ?
3(√2+1)^2010+1/(√2-1)^2010
= [3(√2+1)^2010(√2-1)^2010 +1 ] / D
= [3((√2+1)(√2-1))^2010 +1 ] /D
= [3(1)^2010 +1 ] /D
= 4/D
donc (4)= 2/((√2-1)^1005)=2*(√2+1)^1005
peut se mettre sous la forme a+b√2, y a un autre cheminement ?
Re: racine carrée (défi de la classe de Seconde)
par mathelot » 23 Déc 2018, 16:18
ok pour la (4),on trouve:
^{1005})
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 23 Déc 2018, 17:05
(5) = (2^2010+1)/√2 : identités (a-b)(a+b) puis (a+b)²
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 25 Déc 2018, 10:17
(6) en mettant 2^2008 en facteur pour les deux termes de la racine, on arrive à 2^2008*cst facilement
le second terme peut aussi être changé en 2^2012-2^2011 = 2^2011....
le second terme peut aussi être changé en 2^2012-2^2011 = 2^2011....
Re: racine carrée (défi de la classe de Seconde)
par Pisigma » 25 Déc 2018, 16:19
Bonjour,
en réécrivant l'expression 8 sous la forme :
+\sqrt{3} ][ (\sqrt{1}+\sqrt{2})-\sqrt{3}] [ \sqrt{3}+(\sqrt{2}-\sqrt{1})] [ \sqrt{3}-(\sqrt{2}-\sqrt{1}) ]})
et en utilisant l'identité remarquable(a-b)=a^2-b^2)
, il vient
]}=2\sqrt{2})
en réécrivant l'expression 8 sous la forme :
et en utilisant l'identité remarquable
Re: racine carrée (défi de la classe de Seconde)
par pascal16 » 25 Déc 2018, 20:52
(7) un développement tout bête donne des termes
(9) on utilise encore 2^(n+1)-2^n = 2^n
(10) (√2)²=2
le tour est fini
Merci Mathelot pour cette petite récréation
(9) on utilise encore 2^(n+1)-2^n = 2^n
(10) (√2)²=2
le tour est fini
Merci Mathelot pour cette petite récréation
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :