Que des "1" ! (un classique)

[le_fabien]

Bonjour,
Simplement si la partie décimale ne comporte que des "1" alors cette partie décimale peut s'écrire comme la somme de puissance de 10.
Exemple: 3,1111111...=3+
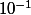
Puis nous avons une somme de termes d'une suite géometrique de raison alors pour n "1" 3,11111...11111=3+
En passant à la limite on a 3,1111111.....=3+=3+

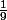
[ThSQ]

Comment peut-on caractériser simplement les nombres qui sont diviseurs d'un entier dont l'écriture décimale ne comporte que des "1" ?

On regarde son dernier chiffre :langue: !


@LEFAB11 : je pense que tu as traité un autre exo.

[le_fabien]

On regarde son dernier chiffre :langue: !


@LEFAB11 : je pense que tu as traité un autre exo.

ouais je sais mais j'avais envie de parler de ce truc que j'aime bien. :zen:

[ThSQ]

Je vois que certains ont une culture encyclopédique !

Oui en l'occurrence le caractère encyclopédique se résume à savoir que si on met 11 encyclopédies sur 10 étagères alors 1- bon courage pour le prochain déménagement 2- il y a une étagère avec au moins deux encyclopédies !

Et mon petit exo de somme presque égale à une puissance... ? :zen:

Dès que j'ai le temps (dans un an, ou deux :briques: )

[leon1789]

Comment peut-on caractériser simplement les nombres qui sont diviseurs d'un entier dont l'écriture décimale ne comporte que des "1" ?

cela se traduit par 10 inversible modulo 9n , i.e. 1=pgcd(9n,10)=pgcd(n,10)
non ?

on peut même donner le nombre de 1 minimum. :id:

[leon1789]

ok ! :happy2:

le nombre est donc caractérisé par le fait d'avoir comme chiffre des unités 1 ; 3 ; 7 ou 9

... et le nombre minimum de 1 est l'ordre multiplicatif de 10 modulo 9n

Les nombres n les plus coriaces sont les puissances de 3. :id:
si n=3^k alors le plus petit multiple de n s'écrivant avec uniquement des 1 est 1111...111 (n fois)

[ThSQ]

... et le nombre minimum de 1 est l'ordre multiplicatif de 10 modulo 9n

Chuis pas sûr qu'on sache calculer ça si facilement. Si ? U(Z/nZ) est assez capricieux m'a-t-on dit.

Par contre ce qui est clair c'est que marche :zen:

[leon1789]

Chuis pas sûr qu'on sache calculer ça si facilement. Si ? U(Z/nZ) est assez capricieux m'a-t-on dit.

oui, au niveau calcul, c'est pas efficace.

Mais en tout cas, l'ordre de 10 modulo 9n est bien le plus petit exposant (pour la relation d'ordre < , ou multiplicativement parlant)

Par contre ce qui est clair c'est que marche :zen:

oui, est un multiple de l'ordre de 10 modulo 9n.

remarque se calcule en factorisant n , non ? (efficacité limitée too, mais c'est moins pire que calculer l'ordre de 10 :zen: )

[SimonB]

Le Cours d'algèbre de Michel Demazure (introuvable dans le commerce...) offre, si mes souvenirs sont bons, une analyse sur ce sujet.

[leon1789]

Le Cours d'algèbre de Michel Demazure (introuvable dans le commerce...) offre, si mes souvenirs sont bons, une analyse sur ce sujet.

je l'ai : je vais regarder

[ThSQ]

Mais en tout cas, l'ordre de 10 modulo 9n est bien le plus petit exposant

Par définition non ?

remarque se calcule en factorisant n , non ? (efficacité limitée too, mais c'est moins pire que calculer l'ordre de 10 :zen: )

Dans les cas pratiques (qui te sont chers ) c'est souvent immédiat.

Je ne sais pas s'il existe des algos pour calculer phi sans passer par la factorisation. Beau sujet d'étude. (***)


Le Demazure dont vous parlez c'est ce livre-ci : http://www.eyrolles.com/Sciences/Livre/cours-d-algebre-9782842250003 ?


Edit : (***) question stupide à laquelle je me réponds : connaissant phi(n) et n=p*q on peut en déduire la factorisation de n donc bon, calculer phi doit pas être simple ..... :stupid_in :marteau:

[SimonB]

Le Demazure dont vous parlez c'est ce livre-ci : http://www.eyrolles.com/Sciences/Livre/cours-d-algebre-9782842250003 ?

Celui-là même ! Un très bon bouquin par ailleurs.

[leon1789]

Le Cours d'algèbre de Michel Demazure (introuvable dans le commerce...) offre, si mes souvenirs sont bons, une analyse sur ce sujet.

sur le bouquin, je cite

Lorsque l'ordre de a est assez petit, on peut le déterminer par énumération brutale des puissances de a

Ce qui laisse entrevoir qu'il n'y a pas d'algo efficace (et même pire !).

On ne connait pas la complexité du calcul de . Elle est sans doute élevée puisque liée à celle de la décomposition en facteurs premiers.

...comme disait ThSQ.