Quatre cercles pour un quadrilatère

par **Imod** » 21 Mai 2008, 23:00

Un problème amusant dont je n'ai pas la solution mais dont je suppose qu'elle doit tenir en quelques lignes :zen:

On trace sur chaque côté d'un quadrilatère convexe un disque dont le côté est un diamètre . Montrer que le quadrilatère est recouvert par les quatre disques !

Imod

par **ffpower** » 21 Mai 2008, 23:04

C est important le convexe?car je vois pas de contrex a priori

par **nodgim** » 22 Mai 2008, 06:13

Les segments qui relient les milieux des cotés sont toujours plus courts que la somme de la moitié des 2 cotés auxquels ils sont reliés.

par **lapras** » 22 Mai 2008, 06:23

J'ai peut etre une solution plutôt courte...
On a juste à créer O1, O2,..O4 les milieux donc les centres des cercles.
On crée le parralélogramme O1O2O3O4
On utilise l'inégalité triangulaire (on raisonne par l'absurde)
on a plus qu'à montrer que pour tout point dans un PG, si on somme les distances de ce point aux sommets, alors cette somme est <= au périmetre de ce parralélogramme.
Pour le démontrer j'utilie cauchy swartz et pythagore... :we:

par **nodgim** » 22 Mai 2008, 06:54

Plus précisement: on partage le quadri en 4 aires départagées par les lignes qui relient les milieux des cotés opposés. Les 2 demi disques associés à chacune de ces aires la recouvre, car ils sont sécants en dehors de cette aire (juste sur le pourtour pour un carré).

par **skilveg** » 22 Mai 2008, 08:19

J'ai peut-être une solution encore plus courte :id: Si on note

et

les points considérés, et qu'on pose

, on a

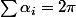
, donc il existe

tel que

. Ce qui revient précisément à dire que

est dans le disque de diamètre

.

par **scelerat** » 22 Mai 2008, 12:49

Si on prend un triangle ABC, le deuxieme point d'intersection des deux cercles de diametres AB et AC est H sur le cote BC (c'est une construction simple de la hauteur AH). A partir de la, c'est evident...

par **Imod** » 22 Mai 2008, 14:15

Merci pour toute ces réponses . J'aime particulièrement celle de Skilveg , vraiment jolie :++: . Mais elle ne marche pas si le quadrilatère n'est pas convexe .

Pour répondre à fpower je n'ai pas trouvé d'exemple de quadrilatère dont les quatre disques ne recouvrent pas son enveloppe convexe : en existe-t-il ?

Imod

par **scelerat** » 22 Mai 2008, 14:31

Imod a écrit:Pour répondre à fpower je n'ai pas trouvé d'exemple de quadrilatère dont les quatre disques ne recouvrent pas son enveloppe convexe : en existe-t-il ?

Son enveloppe convexe est un triangle dont deux cotes appartiennent au quadrilatere, et puisque les deux disques correspondants recouvrent ce triangle...

par **Patastronch** » 22 Mai 2008, 14:46

scelerat a écrit:Son enveloppe convexe est un triangle dont deux cotes appartiennent au quadrilatere, et puisque les deux disques correspondants recouvrent ce triangle...

Et pour les quadrilateres de type ABDC ?

par **ffpower** » 22 Mai 2008, 14:50

lol...je pense que sa methode marche aussi:les triangles ABD et ABC sont contenus dans les cercles

par **Imod** » 22 Mai 2008, 15:18

Bon , ça marche dans tous les cas et il est plus intéressant si on retire la convexité des hypothèses initiales :++:

Imod

par **ffpower** » 22 Mai 2008, 16:20

et manifestement c est la strategie de scelerat qui semble la plus adequate pour etudier tous les cas..

par **skilveg** » 22 Mai 2008, 19:37

Vous êtes sûrs que ce que je raconte ne marche pas pour un quadrilatère quelconque? Un des angles doit quand même être de valeur absolue plus grande que

...

par **Imod** » 22 Mai 2008, 21:24

En tout cas ce n'est plus évident , les angles pouvant se chevaucher !!!

Imod

Quatre cercles pour un quadrilatère

Quatre cercles pour un quadrilatère

Qui est en ligne