Pour prolonger la discussion d'hammana
Un quadrilatère ABCD est convexe et ses côtés sont partagés en p segments égaux (p entier supérieur ou égal à 3).
En reliant les points comme ci-dessous, on obtient un quadrilatère EFGH.
Quel est, en fonction de p, le rapport de l'aire de EFGH sur l'aire de ABCD ?
[img][IMG]http://img211.imageshack.us/img211/5161/18659858.gif[/img]
Quadrilatère partagé en k² parties
12 messages
- Page 1 sur 1
Matt_01 a écrit:En utilisant la formule de l'aire d'un triangle sous forme d'une norme de produit vectoriel, ca vient assez rapidement.
Bonjour
Quelques autres pistes:
On peut s'intéresser aux diagonales de ces deux quadrilatères.
Par exemple:
et l'aire d'un quadrilatère convexe est égale au demi-produit des diagonales multiplié par le sinus de l'angle qu'elles forment .
Ou alors, on fait comme cela a été montré dans une autre discussion pour p=3, en utilisant les deux figures ci-dessous
S aire de ABCD
a+b=S/p
(x+y)(p-1)=S-S/p donc x+y=S/p
aire du quadrilatère noir=S-S/p-S/p=S(p-2)/p
on recommence dans l'autre sens, après avoir montré que tous les segments sont régulièrement gradués par le quadrillage
Finalement aire de EFGH =
[img][IMG]http://img811.imageshack.us/img811/3975/az1.gif[/img]
[/IMG]

Bonjour !
Le quadrilatère étant partagé en parties égales, horizontalement et verticalement, On peut démontrer que quand il se déforme:
1 - Les segments horzontaux sont partagés en parties égales par les segments verticaux et inversement
2 - La somme des aires relatives (par rapport à l'aire totale du quadrilatère) de deux bandes verticales symétriques (bandes jaunes) est la même pour toutes les paires symétriques, il en est de même pour les paires symétriques horizontales.
3 - Pour une bande donnée, la somme des aires relatives de deux quadrilatères (verts) est la même pour toutes les paires symétriques de la bande
4 - La somme des aires relatives de 4 quadrilatères symétriques (rouges) est la même pour tous les groupes de 4 quadrilatères symétriques.
Quelques points de repère pour la conduite des calculs:
Le quadrilatère ABCD est défini par les 3 vecteurs :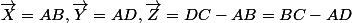 .
.
L'aire de ce quadrilatère est égale à:
/2)
Soient E un point de AB, et G un point de DC tels que AE/AB=DG/DC=p
Soient H un point de AD et F un point de BC tels que AH/AD=BF/BC=q
Soit I l'intersection de EG et HF
L'aire du quadrilatère AEIH est égale à
/2)
N.B. L'astérisque remplace le chapeau (produit vectoriel)

Le quadrilatère étant partagé en parties égales, horizontalement et verticalement, On peut démontrer que quand il se déforme:
1 - Les segments horzontaux sont partagés en parties égales par les segments verticaux et inversement
2 - La somme des aires relatives (par rapport à l'aire totale du quadrilatère) de deux bandes verticales symétriques (bandes jaunes) est la même pour toutes les paires symétriques, il en est de même pour les paires symétriques horizontales.
3 - Pour une bande donnée, la somme des aires relatives de deux quadrilatères (verts) est la même pour toutes les paires symétriques de la bande
4 - La somme des aires relatives de 4 quadrilatères symétriques (rouges) est la même pour tous les groupes de 4 quadrilatères symétriques.
Quelques points de repère pour la conduite des calculs:
Le quadrilatère ABCD est défini par les 3 vecteurs :
L'aire de ce quadrilatère est égale à:
Soient E un point de AB, et G un point de DC tels que AE/AB=DG/DC=p
Soient H un point de AD et F un point de BC tels que AH/AD=BF/BC=q
Soit I l'intersection de EG et HF
L'aire du quadrilatère AEIH est égale à
N.B. L'astérisque remplace le chapeau (produit vectoriel)

hammana a écrit:Bonjour !
Le quadrilatère étant partagé en parties égales, horizontalement et verticalement, On peut démontrer que quand il se déforme:
1 - Les segments horzontaux sont partagés en parties égales par les segments verticaux et inversement
2 - La somme des aires relatives (par rapport à l'aire totale du quadrilatère) de deux bandes verticales symétriques (bandes jaunes) est la même pour toutes les paires symétriques, il en est de même pour les paires symétriques horizontales.
3 - Pour une bande donnée, la somme des aires relatives de deux quadrilatères (verts) est la même pour toutes les paires symétriques de la bande
4 - La somme des aires relatives de 4 quadrilatères symétriques (rouges) est la même pour tous les groupes de 4 quadrilatères symétriques.
Toutes les propositions ci-dessus découlent de la suivante:
Les aires des quadrilatères successifs le long d'une bande quelconque forment une progression arithmétique.
Il en est de même le long d'une diagonale lorsqu'il ya le même nombre de divisions horizontalement et verticlement.
Imod a écrit:C'est un peu ce que j'avais dit sur l'autre fil :we:
Pour revenir à l'élémentaire , avec la configuration suivante :et
.
Imod
Salut
J'arrivais à la même chose, aux notations près.
Si on a les quatre égalités:
alors le point d'intersection O est le barycentre de {(A,(1-h)(1-k)),(B,k(1-h)),(C,kh),(D,h(1-k))}
O est aussi le barycentre {(E,1-h),(G,h)} et de {(H,1-k),(F,k)}
et on a

As-tu déjà calulé le rapport aire(AEOH)/aire (ABCD) ?
chan79 a écrit:il ne dépend pas que de h et k mais aussi du quadrilatère ABCD ...
Je faisais référence aux résultats que j'ai donné précédemment:
"Quelques points de repère pour la conduite des calculs:"
Ils sont très importants pour moi prcequ'à partir de ces résultats on peut écrire facilemet un progamme qui donne sous forme de tableau l'aire de tous les quadrilatères élémentaires, mais je me rend compte qu'ils sont dificilement exploitables dans des calculs manuels.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

