Moi j'aurais tendance a démontrer que f est infiniment dérivable en deux étapes:
(1) on montre qu'elle est infiniment dérivable la ou elle ne s'annule pas.
(2) elle est infiniment dérivable ou elle s'annule.
Pour (1) je montre que pour tout n dans N , si g est infiniment dérivable alors
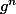
l'est aussi. Et comme g ne s'annule pas sur l'intervalle étudiée alors

est infiniment dérivable. Par suite on a que si g est infiniment dérivable alors

l'est aussi avec Z entier relatif.
Aussi je montre que si

et

sont infiniment dérivables alors

est aussi infiniment dérivable.
Ceci étant fait j'attaque le problème:
p et q sont 1er entre eux donc il existe deux entier relatifs u et v tel que up+vq=1
Or daprès nos lemmes précédant
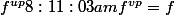
est infiniment derivable la ou elle ne s'annule pas.
Reste plus qu'a montrer que f est infiniment dérivable la ou elle s'annule.
Qu'en pensez vous jusque la ?
une application. On suppose qu'il existe p et q premiers entre eux tels que les applications
et
sont infiniment dérivables.
