Propriété caractéristique du parallélogramme

[hammana]

Montrer que:
Si la somme des carrés des côtés d'un quadrilatère est égale à la somme des carrés de ses diagonales, ce quadrilatère est nécessairement un parrallélogramme.

[Imod]

Bonsoir :we:

Analytiquement c'est complètement évident .

Notons ABCD le quadrilatère et choisissons un repère dont l'axe des abscisse est porté par (AC) et dont l'origine est le milieu O de [AC] . Alors A(-a,0) , B(x,y) , C(a,0) et D(z,t) et l'égalité s'écrit : (x+z)²+(y+t)²=0 c'est à dire que B et D sont symétriques par rapport à O .

Il y a sûrement une façon plus géométrique de voir les choses .

Imod

[chan79]

Bonsoir :we:

Analytiquement c'est complètement évident .

Notons ABCD le quadrilatère et choisisson un repère dont l'axe des abscisse est porté par (AC) et dont l'origine est le milieu O de [AC] . Alors A(-a,0) , B(x,y) , C(a,0) et D(z,t) et l'égalité s'écrit : (x+z)²+(y+t)²=0 c'est à dire que B et D sont symétriques par rapport à O .

Il y a sûrement une façon plus géométrique de voir les choses .

Imod

Bonsoir
Le théorème de la médiane permet d'aboutir assez vite
Si I est le milieu de [AC] et J le milieu [BD]
BA²+BC²=2BI²+AC²/2 (ligne 1)
DC²+DA²=2DI²+AC²/2 ( ligne 2)
IB²+ID²=2IJ²+DB²/2 (ligne 3)
2IB²+2ID²=4IJ²+DB² (ligne 4) obtenue en multipliant la ligne 3 par 2
en ajoutant les lignes 1, 2 et 4
BA²+BC²+DC²+DA²=4IJ²+AC²+DB²
Donc IJ=0
Les diagonales se coupent en leurs milieux
Du coup, on a aussi la réciproque

[hammana]

Bonsoir
Le théorème de la médiane permet d'aboutir assez vite
Si I est le milieu de [AC] et J le milieu [BD]
BA²+BC²=2BI²+AC²/2 (ligne 1)
DC²+DA²=2DI²+AC²/2 ( ligne 2)
IB²+ID²=2IJ²+DB²/2 (ligne 3)
2IB²+2ID²=4IJ²+DB² (ligne 4) obtenue en multipliant la ligne 3 par 2
en ajoutant les lignes 1, 2 et 4
BA²+BC²+DC²+DA²=4IJ²+AC²+DB²
Donc IJ=0
Les diagonales se coupent en leurs milieux
Du coup, on a la réciproque

On dit que la relation BA²+BC²+DC²+DA²=4IJ²+AC²+DB² est due à Euler.

Le site suivant contient toutes les considérations géométiques qu'on peut faire à ce sujet

http://www.apmep.asso.fr/Somme-des-carres-des-cotes-d-un

On peut compléter cet exercice par deux petites questions:

Etant donnés 3 points fixes A, B, C, quel est le lieu géométrique des poinst M tels que:
MA² + MB² + MC² soit constant ?

quel est le lieu géométrique des poinst M tels que:
MA² + MB² - MC² soit constant ?

[chan79]

On dit que la relation BA²+BC²+DC²+DA²=4IJ²+AC²+DB² est due à Euler.

Le site suivant contient toutes les considérations géométiques qu'on peut faire à ce sujet

http://www.apmep.asso.fr/Somme-des-carres-des-cotes-d-un

On peut compléter cet exercice par deux petites questions:

Etant donnés 3 points fixes A, B, C, quel est le lieu géométrique des poinst M tels que:
MA² + MB² + MC² soit constant ?

quel est le lieu géométrique des poinst M tels que:
MA² + MB² - MC² soit constant ?

juste pour le fun, un truc du même genre
3 points A, B et C étant donnés, si on place les points M vérifient MA.MB.MC=constante et si on fait varier la constante, on peut se retrouver face à une tronche d'extraterrestre !
[img][IMG]http://img823.imageshack.us/img823/1393/bc703cassiniemme.gif[/img]

Uploaded with ImageShack.us

[hammana]

Eant donnés 3 points fixes A, B, C, quel est le lieu géométrique des poinst M tels que:
MA² + MB² + MC² soit constant ?

quel est le lieu géométrique des poinst M tels que:
MA² + MB² - MC² soit constant ?

Comme personne ne commente mes deux petites questions, voici une solution inhabituelle de la première:
Quel est le lieu géométrique des poinst M tels que MA² + MB² + MC² soit constant ?

Soi A1 le millieu de BC, B1 le milieu de AC, C1 le milieu de AB. En appliquant le théorème de la médiane (auquel fait référence Chan plus haut) aux triangles MAB, MBC et MCA je montre que si

MA² + MB² + MC² reste constant, MA1² + MB1² + MC1² reste aussi constant.

Je peux donc remplacer A, B, C par A1, B1, C1 dans la recherche du lieu géométrique. En répétant indéfiniment cette opération, mon triangle se réduit au point de concours des médianes. Le lieu cherché est donc le cercle centré en ce point et passant par M.

Cherchons s'il y a une solution du même genre pour la 2ème question

[chan79]

Etant donnés 3 points fixes A, B, C, quel est le lieu géométrique des poinst M tels que:
MA² + MB² + MC² soit constant ?

Salut
Si on remplace les + par des et si on fait varier la constante, on peut se retrouver face à un extraterrestre !!!! :ptdr:
A, B et C sont les points rouges

[img][IMG]http://img845.imageshack.us/img845/9845/cass.gif[/img]

[hammana]

Salut
Si on remplace les + par des et si on fait varier la constante, on peut se retrouver face à un extraterrestre !!!! :ptdr:
A, B et C sont les points rouges

[img][IMG]http://img845.imageshack.us/img845/9845/cass.gif[/img]

C'est très beau Chan! Je vais essayer ça.

Faut-il faire MA²*MB²*MC² ou bien MA*MB*MC=Consstante?
Et puis je ne le ferai pas symétrique, pour faire Picasso!

[chan79]

Faut-il faire MA²*MB²*MC² ou bien MA*MB*MC=Consstante?

je pense que ça revient au même, on fait varier la constante comme on veut

[hammana]

je pense que ça revient au même, on fait varier la constante comme on veut

Je viens justement de réaliser cela

[hammana]

C'est très beau Chan! Je vais essayer ça.

Faut-il faire MA²*MB²*MC² ou bien MA*MB*MC=Consstante?
Et puis je ne le ferai pas symétrique, pour faire Picasso!

Voilà ce que ça donne



Solution du 2nd exercice:

Soit I le milieu de AB. Pour continuer à utiliser le théoème de la médiane j'ajoute le point C' symétrique de C p.r. à I.
MA²+MB²-MC²=MA²+MB²-MC²-MC'²+MC'²=2IA²-2IC²+MC'²=Constante
Le lieu cherché est donc le cercle de centre C' passant par M.
Ces deux exercices apparemment distincts ne sont que 2 cas particuliers d'un même problème que je proposerai dans un autre défi. Le problème général sera peut-être plus facile à résoudre parcequ'il incite à regarder les choses de plus haut.

[hammana]

je pense que ça revient au même, on fait varier la constante comme on veut

Les deux petites questions proposées sont des cas particuliers de l'exercice suivant:

Etant donnés n points quelconques et n coefficients quelconques
Quel est le lieu des points M tels que la somme

reste constante

[hammana]

Les deux petites questions proposées sont des cas particuliers de l'exercice suivant:

Etant donnés n points quelconques et n coefficients quelconques
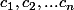
Quel est le lieu des points M tels que la somme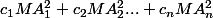

reste constante

Pour clore cette duiscussion:

Soit G le barycentre des points affectés des poids , la somme =Constante peut s'écrire:
=+ =constante, compte tenu du fait que G vérifie la relation=0.

Il en résulte que que la distance GM est constante, le lieu de M est donc un cercle de centre G.
Si la somme est nulle, appelons P le barycentre des points affectés de poids positifs, et N le barycentre de points affectés de poids négatifs, le barycentre est rejeté à l'infini dans la direction PN, le lieu devient une droite perpendiculaire à PN.
Si P et N sont confondus, tout point du plan appartient au lieu.

Dernière remarque, ce résultat n'est qu'une autre forme du théorème de Huygens (ou Steiner) relatif au moment d'inertie d'un corps solide p.r. à un axe