Produit
Olympiades mathématiques, énigmes et défis
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 22 Sep 2006, 18:34
par bitonio » 22 Sep 2006, 18:34
Hello,
Voila un petit exo sympa, qui a été posé aux oraux d'entrées de polytechnique :zen: L'exercice n'est très compliqué en lui même, si on voit le truc

Bonne chance
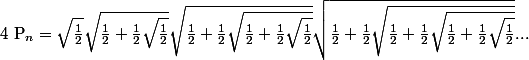
avec n termes
Donner une expression simple de

Calculer la limite de Pn en +oo
Si deja posté toutes mes excuses :we:
Bonne journée
-
oss007
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Sep 2006, 09:39
-
 par oss007 » 22 Sep 2006, 21:20
par oss007 » 22 Sep 2006, 21:20
bonsoir
Ton expression ressemble plus à un produit qu'à une somme.
Ne serait-ce point la formule de Viète donnant l'inverse de pi quand n--->infini? ( vers 1580)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 22 Sep 2006, 21:24
par bitonio » 22 Sep 2006, 21:24
je ne sais pas d'ou ca vient (oui oui c'est un produit!)
ce qui est interessant c'est de trouver l'astuce pour simplifier Pn :)
-
atito
- Membre Relatif
- Messages: 227
- Enregistré le: 10 Sep 2006, 12:46
-
 par atito » 22 Sep 2006, 22:01
par atito » 22 Sep 2006, 22:01
bitonio a écrit:je ne sais pas d'ou ca vient (oui oui c'est un produit!)
ce qui est interessant c'est de trouver l'astuce pour simplifier Pn

Bien deja Essaye de calcluer (Pn)²
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 22 Sep 2006, 22:24
par Flodelarab » 22 Sep 2006, 22:24
Je ne comprends pas bien l'intérêt.
Je crée une suite (Un) telle que:
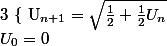
Donc
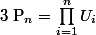
(Un) est une suite qui reste entre 0 et 1 donc la multiplication infinie de ses termes tendra vers 0
non?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 23:22
par tize » 22 Sep 2006, 23:22
Flodelarab a écrit:(Un) est une suite qui reste entre 0 et 1 donc la multiplication infinie de ses termes tendra vers 0
non?
non car on ne peut pas majorer les facteurs par un nombre <1.
les Un se rapprochent de plus en plus de 1...
Contre-exemple :
^n\rightarrow \frac{1}{e}\neq 0)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 23 Sep 2006, 06:22
par bitonio » 23 Sep 2006, 06:22
non non ca tend pas vers 0 :) pas du tout :)
Tize moi j'ai trouvé la solution, j'ai fait cet exo avec mon prof hier en cours de sup :id: Mais bon j'ai trouvé ca marrant, donc je l'ai posté ici...
Sinon Altito, quand j'ai dis je ne sais pas d'ou ca vient, je répond à "Ne serait-ce point la formule de Viète donnant l'inverse de pi quand n--->infini? ( vers 1580)"
Ps: on cherche vraiment une formule simple pour Pn
Allez faite marcher vos neurones :ptdr:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 23 Sep 2006, 09:49
par tize » 23 Sep 2006, 09:49
ce serait donc un produit de cosinus, c'est assez jolie...
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 23 Sep 2006, 11:39
par bitonio » 23 Sep 2006, 11:39
Effectivement

on reconnait dans
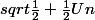
une formule assez connu de trigo non ?
Et si vous calculez
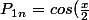.... cos (\frac {x}{2^n}))
vous devriez trouver ce qu'il faut

Bonne chance
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 24 Sep 2006, 07:56
par bitonio » 24 Sep 2006, 07:56
Alors personne ? :doh: Vous allez pas me dire que c'est trop dur quanc même :ptdr:
-
oss007
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Sep 2006, 09:39
-
 par oss007 » 28 Sep 2006, 11:28
par oss007 » 28 Sep 2006, 11:28
bonjour,
cos(a/2^2)....cos(a/2^n) =sin(a)/[(2^n)sin(a/2^n)])
et quand n tend vers + infini : cette expression tend vers :
/a)
ici,
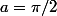
,donc,
le produit infini initial tend vers
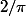
.
Rappel: formule de Viète (1540-1603)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 28 Sep 2006, 18:56
par tize » 28 Sep 2006, 18:56
Comment fait-on pour montrer ça :
cos(a/2^2)....cos(a/2^n) =sin(a)/[(2^n)sin(a/2^n)])
?
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 28 Sep 2006, 20:09
par bitonio » 28 Sep 2006, 20:09
=2sin(a)cos(a))
donc
= \frac {sin(2a) } { 2cos(a) })
maintenant fait le produit et tu vas voir tout se simplifie très très bien !!!

Sinon osss007 c'est correct, bravo ! :++:
Bonne chance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 28 Sep 2006, 23:10
par tize » 28 Sep 2006, 23:10
Merci, comme ça, ca a pas l'air trop compliqué, merci beaucoup
Cordialement
José
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 29 Sep 2006, 19:29
par bitonio » 29 Sep 2006, 19:29
En effet une fois qu'on a vu le truc c'est enfantin, encore faut il le voir :ptdr: c'est un autre problème ca
Bonne soirée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
