Problèmes intéressants/ouverts

[Ruch]

Bonjour à tous.

On va construire le principe suivant: je commence par poster un problème, et le 1er qui le fait en entier et sans aucune erreur, je lui cède la place et ça sera à son tour de proposer un exercice (pas trop infaisable quand même). Chaque fois qu'une personne répond, elle reçoit un certain nombre de points évalué par le concepteur de l'exercice, de 1 jusqu'à 10 points selon sa difficulté (histoire de faire du topic un jeu ^^)

A la base, les exercices que vous allez proposées ne sont pas des "énigmes" à proprement dit, mais plutôt des problèmes du type "ouverts" ou "défis" que l'on trouve dans certains manuels scolaires. Normalement, les connaissances théoriques mathématiques requises vont jusqu'à la terminale et ne doivent pas solliciter des connaissances non acquises jusqu'à cette année.

A vos plots :++:

Edit:
Classement et nombre de points:

1- Quiddam: 2 points.

[Taupin sur Lyon]

Les jeux, c'est po ici je crois !

[Jean_Luc]

Salut,

Le problème c'est que c'est trop facile de tricher si les exos sont connus.

[Ruch]

Je ne savais pas que le problème présent dans mon livre de maths était déjà corrigé sur le net (quoique ce n'est pas exactement la même chose, dans mon exercice il ne s'agit pas du "poker fermé", donc les résultats sont différents.

Et puis, je ne vois pas vraiment l'intérêt de tricher, si ce n'est d'essayer de paraitre fort (et quelle bêtise de vouloir paraitre ainsi...) :hein:

Bien, alors comment chacun de nous va-t-il savoir si le problème est connu ou pas? Au pire, on enlève le système de points, le but n'est pas d'être le meilleur, mais d'apprendre des méthodes de raisonnements un peu moins "scolaires".

Personne n'est partant?

PS: mon problème n'est pas un énigme ^^

[ffpower]

La définition du mot enigme sur le forum est assez large.Disons que ca tend un peu vers exos amusants,interessants..

[Jean_Luc]

Salut,

Et puis, je ne vois pas vraiment l'intérêt de tricher, si ce n'est d'essayer de paraitre fort (et quelle bêtise de vouloir paraitre ainsi...) :hein:

Ce n'est pas exactement ce à quoi je pensais. L'intérêt dans le jeu que tu présentes est de répondre le plus rapidement possible, donc tous les moyens sont bons.

Bien, alors comment chacun de nous va-t-il savoir si le problème est connu ou pas? Au pire, on enlève le système de points, le but n'est pas d'être le meilleur, mais d'apprendre des méthodes de raisonnements un peu moins "scolaires".

Je pense que le système de points est amusant, par contre il faut essayer
de trouver de nouveaux problèmes ou au moins essayer de modifier un minimun ceux qui sont connus.

[Ruch]

Ok. Alors un petit exercice plus ou moins trivial (histoire de s'échauffer ^^)

Démontrer l'égalité suivante (sans faire de calculs, mais avec des raisonnements)

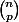= + 2 +

J'espère qu'elle n'est pas présente sur la toile xD.

Etant donné qu'il n'est pas très dur, celui qui y répond aura 2 points.
Il vaut mieux que chacun donne le nombre de points suivant son avis sur la difficulté du problème (le nombre de point pourra aller de 1 à 10 selon la difficulté).

[Dominique Lefebvre]

La définition du mot enigme sur le forum est assez large.Disons que ca tend un peu vers exos amusants,interessants..

En effet! Le genre de démarche proposée par Ruch n'est pas inintéressante, mais n'a pas sa place dans le forum Lycée.

Dominique

[Jean_Luc]

Démontrer l'égalité suivante (sans faire de calculs, mais avec des raisonnements)
= + 2 +

Tu aimes bien les problèmes de dénombrement toi :lol3:

[Ruch]

Et oui, la combinatoire, c'est le seul chapitre que je trouve intéressant pour le moment en terminale :we:
C'est là où les matheux forts en calculs trouvent leur limites^^


Allez, le premier qui trouve et rédige la démonstration aura 2 points (ce n'est pas très dur, au fait)

[Imod]

Allez, le premier qui trouve et rédige la démonstration aura 2 points (ce n'est pas très dur, au fait)

Si on dit que c'est évident en regardant le triangle de Pascal , on mérite un quart des points :we:

Imod

[Jean_Luc]

Pourquoi 1/4 ? moi je dis que ça mérite les 2 points vu que tu t'en es sorti sans faire le calcul des combinaisons.

[Ruch]

:ptdr:

Pour ta belle blague, je te donne points :we:


Edit: Euh Jean luc, une constatation n'est jamais une démonstration^^

[Jean_Luc]

Edit: Euh Jean luc, une constatation n'est jamais une démonstration^^

Si je constate qu'en appliquant 2 fois la formule de Pascal, j'obtiens le résultat, n'est-ce pas une démonstration ?

[Ruch]

Pas vraiment non.

Un petite inspiration (et non un indice) : réfléchissez à comment on démontre par raisonnement que : + = .

[Imod]

D'accord ça ne prouve rien mais bon les calculs ne sont pas inextricables !!! On doit pouvoir le prouver à l'aide de combinaisons mais pourquoi bouder un plaisir simple :zen:



Imod

[AL-kashi23]

D'accord ça ne prouve rien mais bon les calculs ne sont pas inextricables !!! On doit pouvoir le prouver à l'aide de combinaisons mais pourquoi bouder un plaisir simple :zen:



Imod

Moi je ne vois pas de meilleure réponse :we:

[Quidam]

Ok. Alors un petit exercice plus ou moins trivial (histoire de s'échauffer ^^)

Démontrer l'égalité suivante (sans faire de calculs, mais avec des raisonnements)

= + 2 +

J'espère qu'elle n'est pas présente sur la toile xD.

Etant donné qu'il n'est pas très dur, celui qui y répond aura 2 points.
Il vaut mieux que chacun donne le nombre de points suivant son avis sur la difficulté du problème (le nombre de point pourra aller de 1 à 10 selon la difficulté).

Soit n billes numétorées 1 à n.


est le nombre de sous-ensembles de p billes

Parmi eux il y en a qui ne contiennent ni 1 ni 2
Il y en a qui contiennent la bille 1 et pas la 2.
Il y en a qui contiennent la bille 2 et pas la 1.
Il y en a qui contiennent la bille 2 et 1.

Donc :

= + 2 +

[Ruch]

Bien joué Quidam :++:

Tu reçois donc 2 points (je modifierais sans cesse mon poste initial pour récapituler le nombre de points attribués à chaque membre).

Tu es donc invité à poster ton problème.

PS: à la base, les exercices que vous allez proposées ne sont pas des "énigmes" à proprement dit, mais plutôt des problèmes du type "ouverts" ou "défis" que l'on trouve dans certains manuels scolaires. Normalement, les connaissances théoriques mathématiques requises vont jusqu'à la terminale et ne doivent pas solliciter des connaissances non acquises jusqu'à cette année.

[Imod]

Bien joué Quidam :++:

Tu reçois donc 2 points (je modifierais sans cesse mon poste initial pour récapituler le nombre de points attribués à chaque membre).

Tu es donc invité à poster ton problème.

Il me semble que si tu veux t'autoproclamer maître du jeu , il va falloir que tes règles soient claires et précises ( nous ne sommes pas en Birmanie ) . Tu acceptes ou refuses certaines démonstrations à ta guise sans la moindre justification : en quoi la démonstration de Quidam est-elle meilleure que celle d'Imod ( j'adore parler de moi à la 3ème personne ) ?

Imod