Bonjour,
Je me permets de vous soumettre un petit problème de réflexion. Attention, ce n'est pas évident!
Dans une ville en damier (un quadrillage formé par des rues) constituée par n rues parallèles et m rues perpendiculaires, on cherche à se rendre le plus directement possible d'un point A à un point B. Considérons donc A et B comme les sommets opposés d'un rectangle de longueur n et de largeur m. Le chemin le plus direct sera toujours de longueur L = n + m . Exprimer le nombre de chemins possible de longueur L entre A et B en fonction du nombre de rues n et m,
Exemples:
Pour n = 1 et m = 1, nous avons L = 2. Il y a deux chemins possibles.
Pour n = 2 et m = 1, nous avons L = 3. Il y a trois chemins possibles.
Pour n = 2 et m = 2, nous avons L = 4. Il y a six chemins possibles.
Pour n = 3 et m = 2, nous avons L = 5. Il y a dix chemins possibles.
Maintenant, trouver le nombre de chemins dans le cas général.
Bon courage!
Problème de la ville en damier
8 messages
- Page 1 sur 1
Dans une ville (en damier), un quadrillage, formé par des rues, constituée par n rues, parallèles et m rues perpendiculaires(transversal et les rues se traverse de manière perpendiculaire, quel suspens).
On cherche à se rendre le plus directement possible d'un point A à un point B.
tu sous entend que le plus court chemin est en ligne droite, c'est pas du golf?
Considérons donc A et B comme les sommets opposés d'un rectangle de longueur n et de largeur m.
A et B doivent marcher dans leur maison pour aller dans la rue.
Le chemin le plus direct sera toujours de longueur L = n + m . Exprimer le nombre de chemins possible de longueur L entre A et B en fonction du nombre de rues n et m,
on sait que le nombre de rue et le nombre de rue donne la longueur de la ville?
il y a une rue en diagonale de tout manière
Exemples:( cool :-( )
Pour n = 1 et m = 1, nous avons L = 2. Il y a deux chemins possibles.
Pour n = 2 et m = 1, nous avons L = 3. Il y a trois chemins possibles.
Pour n = 2 et m = 2, nous avons L = 4. Il y a six chemins possibles.
Pour n = 3 et m = 2, nous avons L = 5. Il y a dix chemins possibles.
Maintenant, trouver le nombre de chemins dans le cas général.
Bon courage!
test de qi pour nous faire dire que tu as bien dit ta phrase.
On cherche à se rendre le plus directement possible d'un point A à un point B.
tu sous entend que le plus court chemin est en ligne droite, c'est pas du golf?
Considérons donc A et B comme les sommets opposés d'un rectangle de longueur n et de largeur m.
A et B doivent marcher dans leur maison pour aller dans la rue.
Le chemin le plus direct sera toujours de longueur L = n + m . Exprimer le nombre de chemins possible de longueur L entre A et B en fonction du nombre de rues n et m,
on sait que le nombre de rue et le nombre de rue donne la longueur de la ville?
il y a une rue en diagonale de tout manière
Exemples:( cool :-( )
Pour n = 1 et m = 1, nous avons L = 2. Il y a deux chemins possibles.
Pour n = 2 et m = 1, nous avons L = 3. Il y a trois chemins possibles.
Pour n = 2 et m = 2, nous avons L = 4. Il y a six chemins possibles.
Pour n = 3 et m = 2, nous avons L = 5. Il y a dix chemins possibles.
Maintenant, trouver le nombre de chemins dans le cas général.
Bon courage!
test de qi pour nous faire dire que tu as bien dit ta phrase.
Salut,
Chan t'a donné la réponse (8 minutes après la question...) :
Un trajet est formé de n segments horizontaux et de m verticaux donc le choix d'un trajet, c'est le choix des n segments horizontaux (ou des m verticaux) parmi les n+m trajets.
C'est donc le coefficient binomial!}{n!\,m!})
Par exemple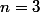 et
et 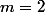 donne
donne 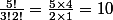
Chan t'a donné la réponse (8 minutes après la question...) :
Un trajet est formé de n segments horizontaux et de m verticaux donc le choix d'un trajet, c'est le choix des n segments horizontaux (ou des m verticaux) parmi les n+m trajets.
C'est donc le coefficient binomial
Par exemple
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
godzylla a écrit:Ce qui est grave est de répondre à des questions sans qu'il soit nécessaire de la poser convenablement.
ton cerveau à corrigé automatiquement le problème.
Oui, les questions non posées ne tiennent pas,
alors on les ramasse ...
godzylla est le pseudo d'un modérateur du forum,
probablement,
mais j'arrive pas à deviner lequel c'est!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
