Problème sur une inégalité

[koddo]

Salut j’ai besoin d’aide pour cet exercice


Prouver que quelque soit les réel a,b et c de l’intervalle ]0 ;1[ on a
a/(b+c+1) +b/(a+c+1) +c/(a+b+1) +(1-a) (1-b)(1-c) < 1
:help:

[Dlzlogic]

Bonjour,
Qu'avez-vous essayé jusqu'à maintenant ?

[Anonyme]

Prouver que quelque soit les réel a,b et c de l’intervalle ]0 ;1[ on a
a/(b+c+1) +b/(a+c+1) +c/(a+b+1) +(1-a) (1-b)(1-c) < 1

Bonjour
comme 0 < a <1 et 0 < b <1 et 0 < c <1
tu peux encadrer les expressions b+c+1 et donc a/b+c+1
Idem pour b/(a+c+1) et c/(a+b+1)

Idem tu peux encadrer 1-a
et donc tu peux déduire un encadrement de (1-a)(1-b)(1-c)

puis tu devrais pouvoir conclure

[Zweig]

La fonction est convexe par rapport à chacune de ses variables sur le cube : elle est donc maximale en l'un des 8 sommets du cube (car continue sur ce dernier). On vérifie sans peine, pour les 8 sommets, que est égale à 1, d'où le résultat.

[koddo]

Bonjour
comme 0 < a <1 et 0 < b <1 et 0 < c <1
tu peux encadrer les expressions b+c+1 et donc a/b+c+1
Idem pour b/(a+c+1) et c/(a+b+1)

Idem tu peux encadrer 1-a
et donc tu peux déduire un encadrement de (1-a)(1-b)(1-c)

puis tu devrais pouvoir conclure

j'ai essayé mais j'ai trouvé( a/b+c+1)+(b/a+c+1) +(c/a+b+1)+(1-a)(1-b)(1-c)< 4

[koddo]

La fonction est convexe par rapport à chacune de ses variables sur le cube : elle est donc maximale en l'un des 8 sommets du cube (car continue sur ce dernier). On vérifie sans peine, pour les 8 sommets, que est égale à 1, d'où le résultat.

Merci y'at il pas une autre méthode plus simple

[Anonyme]

j'ai essayé mais j'ai trouvé (a/b+c+1)+(b/a+c+1) +(c/a+b+1)+(1-a)(1-b)(1-c)< 4

0 < a < 1
et
0 < b+c+1 < 3 donc 0 < 1/b+c+1 < 1/3

donc 0 < a/b+c+1 < 1/3

donc 0 < a/b+c+1)+(b/a+c+1) +(c/a+b+1) < 1

Comme -1 < (1-a)(1-b)(1-c) < 0

à mon avis (a/b+c+1)+(b/a+c+1) +(c/a+b+1) + (1-a)(1-b)(1-c) < 1

[Zweig]

-1 < (1-a)(1-b)(1-c) < 0

0 < a < 1

Rappel de Cinquième : Un produit de réel positifs ne peut pas être négatif

Sinon pour l'auteur, y a pas vraiment plus simple ...

[Anonyme]

Comme 0 < a < 1
on a donc -1 < -a < 0 et donc 0 < 1-a < 1
et donc j'ai fait ce qu'on appelle une boulette !

"Errare humanum est, perseverare...."

@koddo
désolé pour cette erreur grotesque....
Je "promets" de m'inscrire l'année prochaine (car cette année c'est trop tard) et de suivre les cours de maths d'une classe de 5ième.... et de revenir l'année prochaine montrer à tous mes progrès en maths....

[Zweig]

Pas de problème. Cela dit, pas besoin de faire l'ermite pendant 1 an, la section Collège est bien modérée par Lostounet qui se fera un plaisir de répondre à toutes tes interrogations.

[Anonyme]

Pas de problème. Cela dit, pas besoin de faire l'ermite pendant 1 an, la section Collège est bien modérée par Lostounet qui se fera un plaisir de répondre à toutes tes interrogations.

Je ne comprends pas ta réaction...
C'est uniquement de la provocation gratuite..
Alors basta, on est 2 personnes adultes et "civilisées" qui changent de trottoir pour ne pas se croiser...

[vincentroumezy]

"""civilisées"""

[koddo]

Rappel de Cinquième : Un produit de réel positifs ne peut pas être négatif

Sinon pour l'auteur, y a pas vraiment plus simple ...

On a : 0<a<1 ;0<b<1 et 0<c<1
Donc 0< b+c+1 <3 ce qui donne 0<a/(b+c+1)<1/3
De même 0<b/(a+c+1)<1/3
0<c/(a+b+1)<1/3
D’où 0<a/(b+c+1) +b/(a+c+1) + c/(a+b+1)<1 (I)
0<a<1 donc -1<-a<0 ce qui donne 0<1-a<1 de même 0<1-b<1 et
0<1-c<1 d’où 0< (1-a)(1-b)(1-c) <1 (II)
En additionnant (I) et (II) on obtient 0<a/(b+c+1) +b/(a+c+1) + c/(a+b+1) + (1-a)(1-b)(1-c) <2

[Anonyme]

@koddo
Ton raisonnement est correct mais pas suffisant car il faut arriver à démontrer
a/(b+c+1) +b/(a+c+1) + c/(a+b+1) + (1-a)(1-b)(1-c) <1 ( et non pas < 2)
donc il faut chercher une autre méthode.
Comme cette expression est "symétrique" en a, b et c , on peut , peut être , "utiliser" cette propriété ?
mais hélas, pour l'instant je ne vois pas ce qu'il faut "faire" et donc je ne peux pas t'aider d'avantage....

[Olympus]

On a : 0<a<1 ;0<b<1 et 0<c<1
Donc 0< b+c+1 <3 ce qui donne 0<a/(b+c+1)<1/3

Euh, en inversant, l'ordre s'inverse... De toute façon, fait tendre a vers 1, et b et c vers 0 et tu te retrouveras avec un aberrant 1<1/3 .

Perso, je trouve la méthode de Zweig la plus simple. Sinon, peut-être qu'il est possible de multiplier le tout par (a+b+1)(b+c+1)(c+a+1), développer, puis chercher à exprimer sous forme de combinaison de (1-a), (1-b) et (1-c) plus quelques quantités positives, mais c'est assez bourrin :hein:

[mathlegend]

[quote="schulhof"]0 )
salut Olympus :lol3:

[Anonyme]

@mathlegend
C'est vrai : 2 erreurs en 2 messages dans un seul topic: c'est lamentable... .

Je ne cherche aucune excuse..

Je vais cependant essayer d'expliquer : pourquoi ces erreurs.
j'ai fait exactement la même chose que d'autres internautes de MF, j'ai lu l'énoncé du topic , j'ai cru pouvoir répondre en quelques "calculs simples" et j'ai tapé ces calculs qui me semblaient atteindre l'objectif demandé, et j'ai été trop "focalisé" sur le résultat qu'il fallait démontrer...

Et à aucun moment j'ai pris un papier et un stylo pour vérifier ces calculs.
D'où le résultat ==> des grosses erreurs dans les calculs...
Merci pour avoir corrigé ces erreurs de maths.

Question :
Zweig a donné une solution qui n'est pas calculatoire.
N'y a-t-il pas une solution non calculatoire plus simple ?

[Zweig]

Faudrait préciser ce que tu entends par "plus simple". A part en parachutant une réécriture de f qui permette d'affirmer sans rien de plus l'inégalité (si tant est qu'elle existe), je ne vois pas ce qu'on pourrait faire d'autre de plus simple.

[Anonyme]

on ne peut pas passer de R^3 à quelque chose de plus simple vu la symétrie entre les 3 variables a,b et c ?

[Zweig]

On aurait pu se ramener à une inégalité à deux variables si les variables vérifiaient une égalité du style 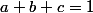, mais là les variables ont vraiment aucun lien entre elles, donc j'vois pas comment on pourrait se ramener à une inégalité à deux variables.

Mais par symétrie, on peut toujours supposer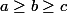 en effet.