Problème pour hachurage d'une zone graphique

[Zorro_X]

R c'est un pourcentage constant pour tous les traits, qui s'applique entre la fin du trait n et le début du trait n+1.

C'est en effet trop simple, je viens de me rendre compte qu'il y a deux solutions à ce système,
1) avec dF>0
2) avec dF<0
Je ne suis pas certain que dF soit le même dans les deux cas...

[Dlzlogic]

R c'est un pourcentage constant pour tous les traits, qui s'applique entre la fin du trait n et le début du trait n+1.

C'est en effet trop simple, je viens de me rendre compte qu'il y a deux solutions à ce système,
1) avec dF>0
2) avec dF<0
Je ne suis pas certain que dF soit le même dans les deux cas...

R n'est pas une différence de Y ? Si c'est un pourcentage, c'est un rapport, alors le rapport de quoi sur quoi ?

DF c'est l'inconnue de l'équation, il ne peut pas y avoir deux solutions suivant le signe de l'inconnue, puisque c'est justement ce qu'on cherche.
En fait, j'aimerais bien savoir le but de cela, par MP si c'est confidentiel.

[Zorro_X]

Il n'y a pas d'autre but que de hachurer graphiquement cette zone, les contraintes sur le hachurage plus rapproché c'est pour un effet d'assombrissement/perspective. Mais je cherche cette solution là et pas une autre.
R est un rapport constant (pourcentage) que ce soit sur X ou sur Y, ca revient au même vu que dF est constante.

[Dlzlogic]

Vous savez, c'est pas vraiment une bonne idée de changer les hypothèses.
Au début, la valeur à trouver était DF. Maintenant c'est une constante.
R était une constante en Y, maintenant c'est un rapport.
Le point de départ de la première hachure et le point d'arrivée de la dernière sont des critères qui ne se justifient que dans des cas très particuliers.

Maintenant votre question est devenue "Comment faire varier l'écartement de hachures en fonction d'un assombrissement recherché ?". Je pense que ça doit faire l'objet d'un autre topic.
Y'a un nouveau mot : perspective. qu'est-ce qu'il vient faire ici.

A relire :

J'avoue que j'osais espérer une réponse un peu plus construite

[Skullkid]

Désolé Zorro_X j'avais aussi mal compris la définition du recouvrement. Du coup en reposant le problème mathématiquement, je ne pense pas qu'il y ait d'expression simple de dF. Dans le cas le plus compliqué, c'est-à-dire celui du dessin que tu as posté, dF est solution d'une équation polynomiale moche dont le degré est fonction de dF (si je ne me suis pas trompé) donc il faut procéder numériquement. Tu dis que la dichotomie prend trop longtemps, est-ce que tu peux essayer de faire tourner l'algorithme suivant, voir s'il est plus efficace (j'ai pas essayé de le coder donc je ne garantis rien) ?

Partant d'un coefficient directeur , tu calcules les n hachures et tu notes 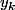l'ordonnée du point d'arrivée de la n-ième hachure. À partir de là tu peux itérer non pas par dichotomie mais en prenant comme nouveau coefficient directeur . En partant de ça donnera peut-être quelque chose de plus rapide... (ce que j'appelle R c'est la distance de recouvrement). Tu arrêtes l'algorithme quand 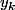est suffisamment proche de 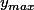, ce qui j'espère finira par arriver !

[Zorro_X]

Dlzlogic, on m'a demandé l'application de mon problème j'ai répondu, le fait qu'il s'agisse d'un effet de perspective, d'un hachurage non-constant, du calcul de l'itinéraire de ton GPS ou de l'âge du capitaine ne change rien au problème... R est un rapport constant, c'est à dire que la hauteur de la zone R dans mon dessin est constante, ça fait en sorte que les traits se rapprochent en haut, lorsque dP commence à entrer en jeu, cela n'a pas changé, je me suis peut être mal exprimé et je m'en excuse si je n'ai pas réussi à expliquer mon problème correctement, mais je n'ai pas changé d'avis entre temps ni modifié le problème.

Skullid, ce que tu me proposes là c'est exactement ma solution "itérative"/algorithmique, t'as juste optimisé mon intervalle "dichotomique" pour approcher plus facilement la valeur visée ce qui en soi n'est pas une mauvaise idée, mais n'empêche que comme ça, même si je réduit le nombre d'itérations d'une façon qui malheureusement reste négligeable vis à vis de la précision à atteindre, ça reste en plus une estimation itérative dont je n'arrive pas à prévoir le nombre d'itérations, le temps que prends la recherche de la solution peut donc être variable et ça m'embête, surtout pour une application graphique où la milliséconde compte...

[Dlzlogic]

Bon, concernant les perspectives, ce qui est important c'est l'angle de la face par rapport à la source lumineuse, généralement le soleil. Il me semble beaucoup plus intéressant de résoudre cela en jouant sur les couleurs, et c'est très facile.
Dans ce domaine, le traitement du problème des faces cachées me parait infiniment plus long qu'un petit calcul par dichotomie.
Dans tous les cas, un calcul de hachures est long à cause du calcul des intersections avec les côtés de polygone.
J'ai l'impression que les impositions, départ de la première hachure, arrivée de la dernière, décalage (recouvrement) sont justifiées à cause du voisinage de deux zones. C'est la raison pour laquelle j'ai parlé la première fois de ce problème lié à "Bird". Là, la difficulté, c'est que le pas est un nombre entier, et c'est effectivement un problème difficile.

[Zorro_X]

Bon, pour les perspectives oublions ça, cela n'apporte pas grand chose à la résolution du problème. Par contre tu tiens peut-être quelque chose en parlant de "pas entiers", il s'agit peut-être d'une sorte de "semi-discretisation", je sais, il y a des gens qui font des doctorats sur ces sujets, mais j'espère que ce n'est pas un de ces problèmes "à docteur"...
Enfin, pour en revenir à Skullkid, je ne vois pas pourquoi il y aurait un système dont le degré dépendrait de dF, ça me semble un peu trop poussé, j'avais plutôt l'impression qu'il y aurait une équation de 2d degré ou dans le pire des cas une intégrale à modéliser, ce qui dépasse mes compétences et capacités mathématiques d'informaticien non-matheux... :haasbeen: :look: :crash:

[fatal_error]

On peut voir les choses ainsi:
sur la droite xmax, on nomme les points d'intersection H(i).
On calcule h(i), la hauteur depuis H(i) à ymin.

Calcul de h(i):

avec a le coeff directeur de nos hachures
Calcul de x(i):
X(i) est l'intersection de la droite (P) deq a_px+b_p et de la droite y=h(i)
donc
On remplace dans h :

avec

Calcul de lexpression du terme général de h(n)

On pose

cest une suite ar.geo dont le terme général est donné par

avec
cad


Enfin il reste à égaliser

et comme tu le constates, on a une équation de degré n à résoudre en a (c est fonction de a)

[Skullkid]

Enfin, pour en revenir à Skullkid, je ne vois pas pourquoi il y aurait un système dont le degré dépendrait de dF, ça me semble un peu trop poussé, j'avais plutôt l'impression qu'il y aurait une équation de 2d degré ou dans le pire des cas une intégrale à modéliser, ce qui dépasse mes compétences et capacités mathématiques d'informaticien non-matheux... :haasbeen: :look: :crash:

J'obtiens le même genre d'équation que celle que vient d'écrire fatal_error. Avec ses notations, l'inconnue a est présente dans c, r et n1, ce qui rend l'équation assez moche. Algorithmiquement, on pourrait peut-être résoudre l'équation numériquement pour plusieurs n1 choisis d'avance (pour avoir une vraie équation polynomiale) et vérifier que la solution trouvée redonne le bon n1, mais ça voudrait dire résoudre plusieurs équations de potentiellement haut degré. Peut-être que le nombre d'itérations sera suffisamment réduit dans ce cas, puisqu'on itère sur les valeurs entières possibles de n1.

[Dlzlogic]

Bonjour,
N'oubliez pas que dans le cas de dessin informatique, on ne peut compter que des pixels entiers, donc on ne peut prendre que des fractionnaires.
J'avoue que je ne suis pas sûr d'avoir compris le problème. D'après les hypothèses que j'ai rappelées, mon calcul est-il faux ? ou les hypothèses que j'ai précisées ne sont pas celles-là. J'aimerais bien que FE ou S m'expliquent.

[Zorro_X]

Il ne faut pas prendre en compte le coté discret des pixels, je dessine bien en utilisant des valeurs réelles, mon framework graphique (OpenGL) se charge de convertir cela convenablement en ce qu'il faut pour afficher ce qu'il faut là où il faut. C'est complètement hors sujet, mais il fait une projection sur les pixels et les "remplit" proportionnellement au taux de recouvrement d'un pixel sur la droite (anti-aliasing). En somme, ne vous inquietez pas de cela, il s'agirait d'ajouter des contraintes tout à fait inutiles au système...

[Dlzlogic]

C'est marrant, au lieu d'essayer de profiter de ce qu'on vous explique, vous trouvez toujours moyen de dire qu'on a rien compris. On y est tous passés.
Vous savez, ça fait 30 ans que je fais du dessin informatique, je sais parfaitement qu'on peut donner des valeurs réelles, mais je sais aussi qu'avec un problème tel que le vôtre, de position exacte entre un côté et un autre, la pente qui est un rapport de longueurs etc. ce détail qui vous parait mineur est à prendre en compte.
Rassurez-vous, je ne m'inquiète pas, j'observe qu'on a eu beaucoup de mal à vous comprendre, qu'on en a tous "pris pour notre grade", et même si vous prenez un canon pour tuer une mouche, vous n'arriverez même pas à lui faire peur.

[Zorro_X]

J'essaie juste de cadrer le problème pour éviter de déborder sur des considérations qui ne feraient que le rendre plus complexe. Je ne manifeste aucune agressivité ni manque de considération mais bien au contraire, je suis admiratif face à vos réponses, qui même si elles ne m'arrangent pas, démontrent vos compétences et mettent bien en évidence mes lacunes. Je vous remercie tous pour vos efforts en ce sens, et il ne me semble pas en avoir "donné pour son grade" à qui que ce soit, si c'est le cas je m'en excuse car nul en était mon intention.

Enfin, si cela peut arranger votre compréhension du problème, après m'y être penché un peu plus, peut-être que ceci apportera les précisions qui manquaient à certains parmi vous :
RP etant une valeur réelle comprise entre 0 et 1, fixe.
Avec RP on calcule Xr qui est de longueur constante telle que Xr = (Xmax - Xmin).RP
Enfin R = Xr.dF
R est bien constante sur les n traits à dessiner.

[Skullkid]

Rassure-toi Zorro_X, tu n'as agressé personne.

J'avoue que je ne suis pas sûr d'avoir compris le problème. D'après les hypothèses que j'ai rappelées, mon calcul est-il faux ? ou les hypothèses que j'ai précisées ne sont pas celles-là. J'aimerais bien que FE ou S m'expliquent.

Dlzlogic, si tu parles de ce calcul-là :

J'appelle A le point à Xmin, pour la 5è hachure. Sa projection sur Xmax est C, L'arrivée de cette 5è hachure est B
AC = Xmax-Xmin
BC = (Xmax-Xmin) * DF = e + R ; e est la distance de 2 arrivées de hachures.
Ymax = n * e + BC = n * e + e +R
e = (Ymax + R) / (n+1)
DF = (e + R) / (Xmax - Xmin)

alors il contient la même erreur d'interprétation de R que fatal_error et moi avons faite au début à cause du dessin : e n'est pas une constante car dans la partie haute de la zone (celle où la droite dP se trouve à droite de xmin), R doit être égal à la différence de hauteur entre la fin d'une hachure (sur xmax) et le début de la suivante (sur dP, et pas sur xmin). C'est ce que Zorro_X expliquait en disant que les hachures se rapprochent les unes des autres quand l'ordonnée augmente.

Pour en revenir au problème, ta dernière explication avec RP me fait douter : tu sembles définir R à partir de dF, doit-on comprendre que R ne fait pas partie des contraintes (des arguments de ta fonction de dessin) ? Jusqu'à présent, on a tous considéré que les paramètres connus a priori étaient xmin, xmax, ymax, dP, n et R. A priori, le fait de ne pas connaître R à l'avance ne va pas simplifier la tâche, mais c'est histoire de bien tous parler du même problème.

[Zorro_X]

Rassure-toi Zorro_X, tu n'as agressé personne.
Pour en revenir au problème, ta dernière explication avec RP me fait douter : tu sembles définir R à partir de dF, doit-on comprendre que R ne fait pas partie des contraintes (des arguments de ta fonction de dessin) ? Jusqu'à présent, on a tous considéré que les paramètres connus a priori étaient xmin, xmax, ymax, dP, n et R. A priori, le fait de ne pas connaître R à l'avance ne va pas simplifier la tâche, mais c'est histoire de bien tous parler du même problème.

Merci pour ta remarque Skullkid :we:
R peut s'exprimer de façon constante sur l'axe des X (Xr = (Xmax - Xmin) . RP) donc elle est constante aussi sur l'axe des Y. Ce que j'essayais de montrer là, visiblement maladroitement c'est que si cela arrange quelqu'un de considérer R constant sur l'axe X (Xr), ça l'est aussi... Mais si ça vous embrouille, oubliez ce que j'ai dit, ma tentative de clarification obscurcit peut-être plus qu'elle n'éclaire... :marteau:

[Zorro_X]

Bon, juste pour clore le sujet, je vous remercie tous pour votre implication dans ce sujet. J'ai malheureusement fini par garder ma solution itérative en limitant le nombre d'itérations, même si je n'ai pas atteint la précision souhaitée, tant pis car visuellement ca ne se voit pas trop finalement... mais au moins je garde ma maîtrise sur le temps de calcul...
C'était un de ces problèmes en apparence simple mais qui finit par nous prendre la tête car ca ne l'était pas tant que ca: on finit par avoir l'impression de frôler la solution à tout moment, sans finalement jamais tomber dessus... Grâce à vous j'ai compris pourquoi car vous m'avez montré quelle était la complexité qui en était la cause : MERCI ! :king2: