Tout le principe est de bien décrire l'univers des issues (des événements singletons).
Si j'ai bien compris, on dispose de

jetons dont

sont rouges, et on les distribue tous à Pierre et à Paul
Première question : reçoivent-ils autant de jetons l'un que l'autre ? (auquel cas

est pair)
Seconde question : les jetons sont-ils numérotés (donc différentiables) ?
Je suppose que la réponse est "oui" aux deux questions et on pose
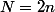
. Pour fixer les idées (ou quitte à renuméroter...), on suppose que les jetons sont d'abord numérotés rouges puis noirs (les jetons
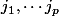
sont rouges, les autres sont noirs)
Du coup, on s'intéresse aux parties de n éléments d'un ensemble en comportant

: chacune de ces parties constitue une issue, et il y a
!}{(n!)^2})
parties donc autant d'issues.
Si la répartition n'est pas truquée, cela donne les probabilités pour une issue : la probabilité d'une issue est exactement égale à
^2}{(2n)!})
Pour savoir si Pierre a reçu le jeton
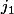
, il suffit de considérer le nombre de parties qui contiennent le jeton
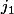
: ce sont exactement les parties constituées de
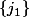
union "

éléments pris parmi
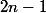
" et l'analyse combinatoire fait le reste.
Si on veut maintenant savoir la probabilité que Pierre ait

jetons rouges (indépendamment de leur numéro), on compte de même le nombre de parties. Une partie de

éléments en comptant

rouges, c'est une partie qui comporte

jetons parmi
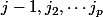
et
)
parmi
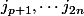
et là aussi un décompte donne le résultat.
Dans tous les cas l'univers est
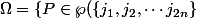 : Card(P)=n\})
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
