Probabilités et (un peu) d'arithmétique

[chombier]

N est un entier naturel non nul. On choisit au hasard un nombre entre 1 et N (équiprobabilité).

On note M3 l'événement : "le nombre choisi est un multiple de 3"
On note M7 l'événement : "le nombre choisi est un multiple de 7"

Pour quelle(s) valeur(s) de N les événement M3 et M7 sont-ils indépendants ?

Que se passe-t-il quand N devient très grand ?

[Monsieur23]

Aloha,

J'imagine qu'il y a une solution plus élégante que de regarder toutes les valeurs de N modulo 21 ?

[chombier]

Aloha,

J'imagine qu'il y a une solution plus élégante que de regarder toutes les valeurs de N modulo 21 ?

Ah je ne suis pas sur qu'il y ait de solutions particulièrement élégante.

Pour être honnête, j'ai présenté cet exercice à l'oral de capes (avec N=50) comme application de la probabilité conditionnelle. (Caculer .

Ils m'ont demande si M3 et M7 étaient indépendants, et je pensais bien que "globalement oui" mais en fait non, et j'ai dit que je pensais que ça devait être vrai pour certaines valeurs de N. Un des membres du jury a affirmé que M3 et M7, quelle que soit la valeur de N, ne seraient pas indépendants.

Pourtant il me semble que pour N=1, N=2 et N multiple de 21, les événements M3 et M7 sont indépendants.

Et que plus N est grand, moins ils sont dépendants (je sais, ce n'est pas très rigoureux, mais je me comprends)

Enfin bref, je ne l'ai pas contredit, évidemment, vu qu'ils sont passés à autre chose. Mais j'ai gardé ça dans un coin de mon crâne.

[Ben314]

Salut,
Si a et b sont premiers entre eux avec b>a, lorsqu'on tire aléatoirement un nombre entre 1 et N, la proba qu'il soit multiple de a est (où 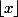désigne la partie entière de x), celle d'être multiple de b est et celle d'être multiple de est .
Il y donc indépendance ssi .
Si on écrit où , et ça donne où
Soit encore .
Si on suppose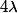 non nul, alors alors que donc et donc. Sauf que, si , alors (car ).
On a donc forcément d'où .
- Si alors et c'est à dire .
- Si alors est multiple de et le fait que signifie uniquement que .

Par exemple, si et les entiers qui marchent sont tout ceux tels que ainsi que ceux de la forme avec c'est à dire .
Ca en fait donc... un certain nombre... et il n'y a pas que les multiples de 21 qui marchent.

[chombier]

Pas mal ! Je n'ai pas tout compris, je devrais, mais l'arithmétique me donne très vite mal à la tête :hum:

Quand utilises tu que a et b sont premiers entre eux ? Quand tu calcules la probabilité d'être un multiple de ab ?

Ensuite tu fais une double division euclidienne, et après je suis un peu largué, j'avoue.

En revanche j'ai fait une simulation avec un tableur, et pour a=3 et b=7, tes prévisions sont parfaitement exactes.

On va dire que je n'ai pas compris ce que disait le juré du capes :lol3:

Je ne sais pas ce qu'il se passe si on met un juré de capes face à son erreur ? Ca doit tellement dépendre du caractère de la personne...

[Ben314]

Le fait que a est b sont premier entre eux, ça sert à dire que [(a divise n) et (b divise n)] équivaut à (ab divise n).