Proba. (avec les boules...)

[Ben314]

Une "amusette" de proba dont l'idée est tiré du forum "supérieur" et dont je n'ai pas la solution pour le moment.
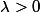
On fixe un réel (plus petit, plus grand... ou égal à 1)
Pour un entier (assez grand), on s’intéresse à l'expérience aléatoire consistant à tirer avec remise (partie entière) boules dans une urne contenant boules différentes.
On note la variable aléatoire correspondant au nombre de boules différentes tirées (comme il y a remise, on risque de tirer toujours la même boule et dans ce cas )
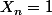
prend donc des valeurs entières entre et
1) Peut on calculer l’espérance de ? sa variance ? (mais c'est pas vraiment ça qui m’intéresse...)
2) La v.a.r. à valeur dans l'intervalle admet elle une limite lorsque tend vers l'infini ? Si oui, quelle est la loi de ?

[Doraki]

A mon avis ça converge vers Y qui suit la loi P(Y=min(1,;))) = 1.


On peut commencer par le cas ;)=1 :

Pour k et n entiers, P(Xn <= k) <= n!/k!(n-k)! * (k/n)^n.

Avec l'approximation de stirling on a un truc du genre
P(Xn/n <= a) = O((a/ (a^a*(1-a)^(1-a)))^n / sqrt(2a(1-a)pi n))
Et pour 0 <= a < 1/2, (a/ (a^a*(1-a)^(1-a)) < 1 donc P(Xn/n <= a) -> 0.

[Ben314]

lorsque avec

Donc la variance tend vers 0...

Edit :
Après calculs,

[beagle]

"Dernière modification par Ben314 Aujourd'hui à 23h03."
t'inquiète Ben, on avait rectifié tout seul...

[Ben314]

c'est le temps qu'il me faut pour calculer une variance...