Presque commutatif
Olympiades mathématiques, énigmes et défis
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 17 Jan 2018, 23:33
par Archytas » 17 Jan 2018, 23:33
Bonsoir,
Petit défi pour les amateurs :
Soit

un groupe et

un sous-groupe d'indice fini

de

. Montrer que si
)
alors
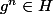
. (où
)
désigne le centre de

)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Jan 2018, 11:32
par Ben314 » 18 Jan 2018, 11:32
Salut,
On vérifie facilement que
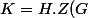=\{hz\,;\;h\!\in\!H\,,\,z\!\in\!Z(G)\})
est un sous groupe de

dans lequel

est distingué.
De plus l'indice

de

dans

est le produit de l'indice

de

dans

par l'indice de

dans

donc

divise

.
Celà signifie que tout élément

du groupe quotient
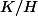
(de cardinal

) vérifie
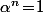
ce qui prouve le résultat vu que
\!\subset\!K)
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 18 Jan 2018, 21:01
par Archytas » 18 Jan 2018, 21:01
Bien joué. Une autre méthode consiste à prendre
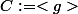
le sous groupe de
)
engendré par

et constater que
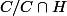
agit librement sur
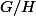
et d'appliquer la formule des classes mais ta solution fonctionne aussi

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités