Premiers entre eux

[Doraki]

Et pour 14^n+11 tu vas rajouter quoi comme condition ?
Et pour 74^n+7563 ?

[Ben314]

boaf...
p'têt que 1 c'est pas un naturel non plus...

[leon1789]

Soient les entiers tels que la suite contienne au moins deux entiers premiers entre eux.
Montrer q'il existe une infinité de nombres de la forme premiers entre eux deux à deux .
:zen:

Considérons n et m des nombres premiers distincts et
montrons que et sont premiers entre eux (ce qui résout le problème puisqu'il existe une infinité de nombres premiers).

Ecrivons l'hypothèse et premiers entre eux.


Soit d un diviseur commun à et .

Alors d est premier avec a (un diviseur commun à "a et d" divise c, donc divise et , donc divise 1)

Ainsi, on obtient , puis par inversibilité de a modulo d,
on arrive à
Comme n et m sont premiers (donc premiers entre eux), il vient

Donc donc d divise et , qui sont premiers entre eux, donc d divise 1.

[leon1789]

Soient les entiers tels que la suite contienne au moins deux entiers premiers entre eux.
Montrer q'il existe une infinité de nombres de la forme premiers entre eux deux à deux .
:zen:

Ecrivons l'hypothèse : et premiers entre eux ( 0<i<j ).

Considérons n et m des nombres premiers distincts et
montrons que et sont premiers entre eux
(ce qui résout le problème puisqu'il existe une infinité de nombres premiers).

Soit d un diviseur commun à et .

Alors d est premier avec a (un diviseur commun à "a et d" divise c, donc divise et , donc divise 1)

Ainsi, on obtient , puis par inversibilité de a modulo d,
on arrive à

Or d est premier avec b (un diviseur commun à "b et d" divise c, donc divise et , donc divise 1)
donc b est inversible modulo d. Et comme n et m sont premiers distincts (donc premiers entre eux),
il vient

Donc donc d divise et , donc d divise 1.

Conclusion : et sont premiers entre eux

[Matt_01]

Or d est premier avec b (un diviseur commun à "b et d" divise c, donc divise et , donc divise 1)
donc b est inversible modulo d. Et comme n et m sont premiers distincts (donc premiers entre eux),
il vient

Sauf erreur, on ne peut conclure cela que lorsque b^n = b^m = 1 mod d.
Par exemple b = 14 en 3 et mod 5.
Sinon je pense qu'on peut considérer que tu as la bonne interprétation du problème (même si MMu nous avait guidé sur l'autre).

[leon1789]

Sauf erreur, on ne peut conclure cela que lorsque b^n = b^m = 1 mod d.
Par exemple b = 14 en 3 et mod 5.

ah oui exact, j'ai vu un =1 fantôme en pensant trop fort à l'ordre de b... :triste:

[Ben314]

De , c'est à dire (si n>m), on ne peut pas déduire grand chose.
Au mieux, en supposant que le groupe multiplificatif (Z/dZ)* est cyclique et que b est un générateur de ce groupe, on en déduit que phi(d) (indicatrice d'euler) divise n-m.

Il me semble que l'exemple de doraki montre que l'énoncé est totalement faux, même en rajoutant l'hypothése n>=1.
Si Un=14^n+11 alors
- U1=25 et U2=207 sont bien premiers entre eux.
- Modulo 5 on a Un=(-1)^n+1=0 pour n impair : les U(2n+1) sont tous multiples de 5
- Modulo 3 on a Un=(-1)^n-1=0 pour n pair : les U(2n) sont tous divisible par 3
Donc dès qu'on prend ne serait-ce que 3 termes de la suites, il y aura forcément deux d'entre eux non premiers entre eux (soit ils seront tout les deux divisible par 3, soit par 5)

Et on peut trouver le même genre de contre exemple avec "plus" de termes premiers entre eux, par exemple se débrouiller pour que les U(7n) soient tous divisible par P0 (premier), que les U(7n+1) soient tous divisible par P1 (premier) ... que les U(7n+6) soient tous divisible par P6 (premier).
D'une telle suite, on tirera au mieux 7 nombres 2 à 2 premier entre eux, mais pas un de plus.

[Matt_01]

Ce que je voulais dire par rapport à l'énoncé, c'est que la preuve de Léon aurait pu montrer qu'il existe une infinité de paires de nombres premiers entre eux (je pensais qu'il voulait montrer cela à la base), et que pour moi c'est la véritable démonstration à faire.

[Ben314]

Et mon "on peut même..." de la fin est sans intérêt vu que c'est ce qu'a déjà fait doraki avec la deuxième suite qu'il donne comme contre exemple :
Si Un=74^n+7563 alors
- U1=7 637=7×1091 ; U2=13 039=13×17×59 et U3=412 787=61×67×101 sont 2 à 2 premiers entre eux MAIS
- Modulo 7 on a Un=4^n+3=0 pour n=3k+1 : les U(3k+1) sont tous multiples de 7
- Modulo 13 on a Un=(-4)^n-3=0 pour n=3k+2 : les U(3k+2) sont tous multiples de 13
- Modulo 61 on a Un=(13)^n-1=0 pour n=3k : les U(3k) sont tous divisible par 61

Et en fait, pour "fabriquer" un contre exemple avec (par exemple) N nombres premiers entre eux et pas plus, il suffit de prendre N nombres premiers p tous de la forme Nk+1 (il en existe une infinité).
Cela assure que les corps Z/pZ contiennent tous des racines primitive N-ième de l'unité et il n'y a plus qu'à en prendre une par corps puis à résoudre un "système chinois" pour déterminer un "b" congru à chacunne des racines primitives choisies modulo chaque p choisis.
On peut prendre le "a" au pif et de nouveau résoudre un système chinois pour trouver le "c" qui va bien.

Question à Doraki : pourquoi tu as pris 7, 13 et 61 plutôt que 7, 13 et 19 ?

[Ben314]

Ce que je voulais dire par rapport à l'énoncé, c'est que la preuve de Léon aurait pu montrer qu'il existe une infinité de paires de nombres premiers entre eux (je pensais qu'il voulait montrer cela à la base), et que pour moi c'est la véritable démonstration à faire.

Sauf que ce qu'a vu doraki, c'est que le résultat est faux, même si on précise n>=1.
Qu'il est toujours faux si on donne des conditions sur a,b,c du style "être au moins égal à..."
Et qu'il reste faux si on suppose non pas qu'il y en a deux dans la suite de premiers entre eux, mais qu'on suppose qu'il y en a trois... ou plus...

Donc là, je vois vraiment pas comment "rectifier le tir" pour avoir un énoncé JUSTE.


P.S. Je sais comment vous fonctionnez vous, mais perso, quand j'ai un contre exemple à un "théorème", ben j'arrête de chercher la "preuve" du théorème... :mur:

[leon1789]

Je récidive en changeant de famille d'exposants...


Ecrivons l'hypothèse : et premiers entre eux ( 0<i<j ).

Considérons la suite (strictement croissante) récurrente définie par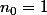 et

Intérêt d'une telle suite ? Pour tous u<v, on a car est multiple de .

Montrons que et sont premiers entre eux...



Soit d un diviseur commun à et .

Alors d est premier avec a (un diviseur commun à "a et d" divise c, donc divise et , donc divise 1)

Ainsi, on obtient , puis par inversibilité de a modulo d,
on arrive à

Or d est premier avec b (un diviseur commun à "b et d" divise c, donc divise et , donc divise 1)
donc b est inversible modulo d.

Et comme (en imposant u<v), il vient

Donc donc d divise et , donc d divise 1.

Conclusion : et sont premiers entre eux.

[Matt_01]

Sauf que ce qu'a vu doraki, c'est que le résultat est faux, même si on précise n>=1.
Qu'il est toujours faux si on donne des conditions sur a,b,c du style "être au moins égal à..."
Et qu'il reste faux si on suppose non pas qu'il y en a deux dans la suite de premiers entre eux, mais qu'on suppose qu'il y en a trois... ou plus...

Donc là, je vois vraiment pas comment "rectifier le tir" pour avoir un énoncé JUSTE.


P.S. Je sais comment vous fonctionnez vous, mais perso, quand j'ai un contre exemple à un "théorème", ben j'arrête de chercher la "preuve" du théorème... :mur:

J'suis bien d'accord, mais on n'a pas exclu le fait qu'il existe une infinité de paires (i,j) telles que ui premier avec uj (sans aucune interaction avec les autres paires), non ? Quand on lit l'énoncé on peut comprendre ça (faut dire qu'il est pas forcément très clair).

[MMu]

Je trouve MMu vraiment nul de vouloir généraliser un problème d'un concours étranger sans approfondir d'avantage les conditions sur les coefficients . :mur: :marteau:

[Doraki]

pourquoi tu as pris 7, 13 et 61 plutôt que 7, 13 et 19 ?

Je cherchais x tel que 1+x+x² contienne 3 facteurs premiers distincts (sans compter 3 parcequ'il donnerait une période de 1), et j'ai pris le plus petit possible (41).

Si j'avais voulu 7,13 et 19 il aurait fallu prendre x = 2 ou 4 mod 7, 3 ou 9 mod 13, et 7 ou 11 mod 19,
ce qui donne x = 102,163,410,520,... mod 1729. Donc plus grand que x=41

---

Il me semble que si on veut savoir quelles suites ab^n+c marchent,
Si b il existe un ensemble infini de membres premiers deux à deux.

Si N > k, il ne peut pas y avoir d'obstruction mod N parceque b^N-1 n'est pas assez gros pour contenir N nombres premiers distincts (sans même devoir se restreindre aux premiers qui sont = 1 mod N), donc si il y a un problème c'est qu'il y a une obstruction avant.

[Ben314]

@doraki : trés bien vu...
@MMu : personne n'est parfait...

[nodjim]

Pour ma part, je suis allé bien trop vite, trop accoutumé que j'étais par la fonction voisine, mais cependant différente, de an²+b. De plus, MMU est assez connu pour présenter des problèmes originaux, et ce n'est pas fréquent qu'il se fasse piéger, ce qui a contribué à baisser ma vigilance. Les erreurs participent aussu à la connaissance...

[Matt_01]

Perso j'ai pas compris ce que Doraki conclue avec le fait que b^n-1 a moins de n facteurs premiers.
J'vois pas comment ca nous construit la suite en fait. Quelqu'un pour m'éclairer ?