Le premier sera le dernier !

[Imod]

Bonsoir :zen:

Un problème que j'ai déjà proposé sur un autre site et qui reste sans réponse

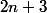
personnes ( entier ) participent à un tournoi d'échecs dont les règles sont les suivantes :

1°) Chaque paire de joueurs se rencontre exactement une fois .
2°) Deux matchs ne sont jamais joués en même temps .
3°) Après avoir disputé une partie chaque joueur est libre pour les parties suivantes .

Montrer qu'un des joueurs ayant participé au match d'ouverture sera aussi invité au match de cloture .

Amusez-vous bien :zen:

Imod

[Clembou]

Je dénombre matchs possibles...

Par contre ce que je comprends pas, c'est pourquoi : "Après avoir jouer sa partie, le joueur est libre pendant n matchs". Je prends l'exemple de 5 personnes dans le tournoi. A un moment, le joueur 1 ne joueura pas deux matchs d'affilés car il y a le match joueur 2 vs joueur 3 et joueur 4 vs joueur 5...

[Imod]

Ou encore et on a l'impression que ça va être facile :id:

Imod

[Imod]

Le nombre de parties de repos est un minimum , un joueur peut se reposer plus longtemps si nécessaire .

Imod

[Clembou]

Je vois le problème sous forme de permutations... Après pour la rédaction, c'est une autre histoire :mur:

[Clembou]

J'ai essayé avec et voilà ce que je trouve comme un cas possible :

- 1 - 2 - R
-------------
1 2 3 4 5
2 3 4 5 1
3 5 1 4 2
4 1 5 2 3
5 4 3 1 4

(1 : Match 1, 2 : Match 2, R : Joueur qui ne joue pas)

Bon courage pour le cas général !

[nodjim]

Tout joueur de Pk ne peut rejouer qu'à partir de P(k+n+1).
L'un des 2 participants J1 et J2 de la première partie P1 pourra rejouer à partir de la partie P(n+2).
Au bout de n+1 parties, 2n+2 joueurs ont joué. Pour la partie P(n+2), il ne reste donc qu'un seul joueur Jd qui n'a pas joué.
A la partie P(n+2), ne peuvent donc participer que les joueurs J1, J2 ou Jd.
Donc l'un des 2 joueurs J1 ou J2 est obligé de jouer sa seconde partie à P(n+2).
En suivant le même raisonnement pour tous les joueurs, il sont tous amenés à jouer, s'ils ont joué la partie Pk, à jouer la partie P(n+k+1).

Nomnbre de parties NP=(2n+3)(2n+2)/2=(2n+3)(n+1)
Période de participation de chaque joueurp=n+2
La division euclidienne de NP/p renvoie un reste unité.
Donc l'un des joueurs J1 ou J2 jouera la dernière partie.

[nodjim]

Tout joueur de la kième partie Pk ne peut rejouer qu'à partir de P(k+n+1).
L'un des 2 participants J1 et J2 de la première partie P1 pourra rejouer à partir de la partie P(n+2).
Au bout de n+1 parties, 2n+2 joueurs tous différentts ont joué. Pour la partie P(n+2), il ne reste donc qu'un seul joueur Jd qui n'a pas joué.
A la partie P(n+2), ne peuvent donc participer que les joueurs J1, J2 ou Jd.
Donc l'un des 2 joueurs J1 ou J2 est obligé de jouer sa seconde partie à P(n+2), l'autre P(n+3).
En suivant le même raisonnement pour tous les joueurs, il sont tous amenés à jouer, s'ils ont joué la partie Pk, à jouer la partie P(n+k+1)ou P(n+k+2).

Nombre de parties NP=(2n+3)(2n+2)/2=(2n+3)(n+1)
Période de participation de chaque paire de joueur (l'un ou l'autre des 2 joueurs) pé=n+2
La division euclidienne de NP/pé renvoie un reste unité.
Donc l'un des joueurs J1 ou J2 jouera l'avant dernière partie, l'autre la dernière.

Exemple pour 7 joueurs n=2
première partie: J1, J2
participation de J1 ou J2 aux parties suivantes: 4 et 5, 8 et 9, ...20 et 21.

[Imod]

Donc l'un des joueurs J1 ou J2 jouera l'avant dernière partie, l'autre la dernière.

Un exemple de tournoi pour n=1 soit 10 parties à disputer par 5 joueurs ( 1;2;3;4;5) ne pouvant jouer 2 parties de suite .

Exemple : 23 ; 45 ; 12 ; 34 ; 15 ; 24 ; 13 ; 25 ; 14 ; 35 .

Le joueur 3 a disputé la première et la dernière partie mais le joueur 2 qui a aussi disputé la première partie ne participe pas à l'avant dernière :doh:

Imod

[nodjim]

Oui, en effet, ça ne marche pas mon truc :triste:
ça m'a l'air bien compliqué, t'es sûr que ça se démontre ?

[Imod]

C'est un problème d'olympiade donc il y a une solution dont j'ai une petite idée , mais c'est pas moi qui cherche :zen:

Imod

[Imod]

Une réponse limpide d'Aldo sur un autre site :zen:

Imod