Premier donc irréductible

par **Imod** » 07 Juil 2009, 10:12

Bonjour :we:

Un curieux problème de polynômes à coefficients entiers :doh:

* 479 est un nombre premier et

est irréductible dans

.
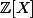
* 2357 est un nombre premier et

est irréductible dans

.

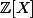
Montrer que si

est premier alors

est irréductible dans

.

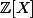
Bon courage :zen:

Imod

par **Maks** » 07 Juil 2009, 11:51

Waow ! :doh:

par **ffpower** » 07 Juil 2009, 13:15

Je plussoie maks..

par **Maks** » 07 Juil 2009, 13:30

J'ai dit une bêtise ?

par **Maks** » 07 Juil 2009, 13:31

On peut dire que

est premier.

par **Maks** » 07 Juil 2009, 13:34

Ben en fait, c'est assez évident, non ?
Si

était réductible, en l'évaluant en

, ça donnerait que

est composé, ce qui est contraire aux hypothèses. Non ?

par **Imod** » 07 Juil 2009, 13:54

Sauf si

avec

ou

. Les coefficients de

et

sont dans

:we:

Imod

par **lapras** » 07 Juil 2009, 13:57

Jolie résultat.
La preuve ne semble pas triviale !

par **Maks** » 07 Juil 2009, 14:08

Imod a écrit:Sauf si avec ou . Les coefficients de et sont dans :we:

Je ne comprends pas.

par **Imod** » 07 Juil 2009, 14:19

Si

alors

ne contredit pas la primalité de

, non ?

Imod

par **Maks** » 07 Juil 2009, 14:20

Ah oui, en effet.

par **Jean-Jack** » 07 Juil 2009, 16:55

En fait, le problème reste vrai pour n'importe quel base b.
Pour la démo, le lemme suivant peut aider :
Toute racine complexe de f a soit une partie réelle négative,soit une valeur absolue plus petite que (1 + rac(4b-3))/2

par **Imod** » 08 Juil 2009, 18:19

En effet il n'y a pas de problème pour la généralisation . On peut d'ailleurs simplifier le lemme sous la forme suivante : toute racine

de

vérifie

.

C'est un peu technique mais sans problème majeur . Le résultat final découle directement de la remarque déjà faite que si

alors

ou

.

Imod

par **leon1789** » 08 Juil 2009, 19:39

J'ai une preuve rapide et tout à fait rationnelle (voir même "entière") du résultat en utilisant le fait que les coefficients de P sont compris entre 0 et b-1.

par **lapras** » 08 Juil 2009, 19:54

Je t'écoute !

par **leon1789** » 09 Juil 2009, 08:25

ma démo est rapide et entière ...ment fausse ! :briques:

par **skilveg** » 09 Juil 2009, 08:58

Le suspense est insoutenable.

par **Imod** » 09 Juil 2009, 22:19

Une démonstration du lemme pour les impatients . Pour le résultat final , j'arrive à conclure avec l'indice déjà donné sauf pour le cas

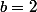
qui m'embête un peu , je vérifierai mes calculs .

Lemme :

Soit

une racine de

avec

l'écriture en base

d'un entier naturel

premier alors

.

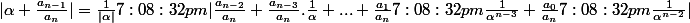
Or pour tout indice

,

et

donc :

Mais d'autre part :

Donc

soit

: contradiction .

Imod

par **lapras** » 09 Juil 2009, 22:40

Effectivement pour n=2 ca suffit pas....

par **leon1789** » 11 Juil 2009, 13:15

http://www.maths-forum.com/showpost.php?p=575498&postcount=18

Imod a écrit:Lemme :

Soit une racine de avec l'écriture en base d'un entier naturel alors .

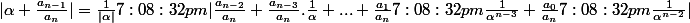
Or pour tout indice , et donc :

Mais d'autre part :

Donc soit : contradiction .

Imod

Comment retrouver l'énoncé un poil plus précis de Jean-Jack ?

Jean-Jack a écrit:le lemme suivant peut aider :
Toute racine complexe de f a soit une partie réelle négative, soit un module plus petit que (1 + rac(4b-3))/2

Il suffit de faire une preuve directe en reprenant l'idée de la preuve d'Imod et ça vient tout seul.

Il arrive de temps en temps que ce genre de situation...

Premier donc irréductible

Premier donc irréductible

Qui est en ligne