Pourquoi toujours neuf ?

[meuchigue]

Salut,

Ce n'est sûrement pas une vraie énigme mathématique et ne me demandez pas comment je suis arrivé à trouver ce résultat (non, je ne suis pas fou !) mais voilà:

Si l'on additionne 9 chiffres consécutifs et que par la suite on additionne chacun des chiffres du résultat de l'addition (plusieurs fois si requis), on retombe toujours sur 9, pourquoi à votre avis ?

Exemple: chiffre de départ (n'importe lequel), exemple :558462

On a donc : 558462 + 558463 + 558464 + 558465 + 558466 + 558467 + 558468 + 558469 + 558470 = 5026194

Donc si on fait la somme de chacun des chiffres de la solution, on arrive à :
(5+0+2+6+1+9+4)=27 et si on continue (2+7)=9.

Vous pouvez essayer et vous verrez que ça tombe toujours (enfin je suppose) sur 9 à la fin ! Pourquoi ??

Merci !

[Zweig]

Soit 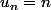. On se fixe un entier et on pose notre somme de départ.

On obtient, comme est une suite arithmétique :

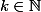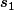Clairement, est paire, i.e, , . D'où . Or il est connu que tout nombre est congru à la somme de ses chiffres modulo 9, i.e, si on appelle la somme des chiffres de , alors :



Si on appelle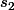 la somme des chiffres de 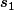, alors on a aussi avec . En réitérant ce procédé, on obtient une suite strictement décroissante d'entiers positifs tous divisibles par 9 qui est nécessairement finie d'après le principe de la descente infinie de Fermat. Comme le plus petit multiple de 9 est lui-même (on ne peut pas avoir une somme de chiffres égale à 0), on arrive nécessairement à un moment donné sur 9 en sommant les chiffres des nombres obtenus.

[L.A.]

Bonjour.

Pour voir que la somme de 9 entiers consécutifs est divisible par 9, on peut aussi dire, en appellant n l'entier du milieu :
S = (n-4)+(n-3)+(n-2)+(n-1)+n+(n+1)+(n+2)+(n+3)+(n+4) = 9n