[MPSI] Polynômes
Olympiades mathématiques, énigmes et défis
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 13 Déc 2010, 10:15
par Euler07 » 13 Déc 2010, 10:15
Salut

-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 13 Déc 2010, 11:23
par Zweig » 13 Déc 2010, 11:23
Salut,
Je pose P(x) = ton polynôme.
Alors
(1-x) = (1-x^2)(1+x^2)\cdots (1+x^{2^n}) = (1-x^4)(1+x^4)\cdots (1+x^{2^n}) = \ldots = 1-x^{2^{n+1}})
D'où
 = \frac{1-x^{2^{n+1}}}{1-x})
(si
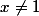
), sinon
 = 0)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 13 Déc 2010, 11:26
par Zweig » 13 Déc 2010, 11:26
Salut,
Je pose P(x) = ton polynôme.
Alors
(1-x) = (1-x^2)(1+x^2)\cdots (1+x^{2^n}) = (1-x^4)(1+x^4)\cdots (1+x^{2^n}) = \ldots = 1-x^{2^{n+1}})
D'où
 = \frac{1-x^{2^{n+1}}}{1-x})
(si
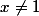
), sinon
 = 2^{2^n})
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 13 Déc 2010, 12:19
par Euler07 » 13 Déc 2010, 12:19
Very good.....
-
Anonyme
 par Anonyme » 13 Déc 2010, 15:17
par Anonyme » 13 Déc 2010, 15:17
Tres astucieux Bravo :zen:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Déc 2010, 16:23
par Doraki » 13 Déc 2010, 16:23
moi quand je développe le polynôme, j'obtiens P(X) = 1+X+X²+X^3...+X^(2^(n+1)-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités

