lynux a écrit:Bonjour, je me permets de poster un petit problème sympa, j'espère qu'il vous plaira et qu'il durera un minimum

Soit
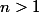
un entier et
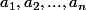
des réels tels que
a_1^2-2na_2 <0.)
Montrer que les racines du polynôme :

ne peuvent pas être toutes réelles.
Salut,
Un résultat classique dit que si P est un polynôme de degré

possédant

racines réelles (comptées avec multiplicité), alors le polynôme P' possède (n-1)racines réelles (comptées avec multiplicité).
En effet, si on note
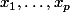
les

racines réelles distinctes de

de multiplicités respectives
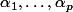
(
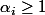
et
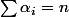
) alors ces nombres seront aussi racines de
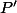
de multiplicité
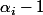
puis grâce au théorème de Rolle, on attrape

autres racines de P' (en appliquant Rolle sur les intervalles
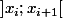
)
Et comme
 = n-1=deg(P'))
, c'est OK.
Pour en revenir au problème, si jamais le polynôme avait

racines réelles, alors en dérivant sucessivement jusqu'a atteindre un degré 2, on obtiendrait un polynôme avec au moins une racine réelle d'après le résultat énoncé ci-dessus (*)
Or en dérivant jusqu'au degré 2, on obtient
! a_1 x + (n-2)! a_2)
de discriminant
!(n-1)! ((n-1)a_1^2 -2na_2))
(après factorisation) qui est alors positif d'après (*) mais ça contredit les hypothèses.
Pseudo modifié : anciennement Trident2.

un entier et
des réels tels que