Polynôme de degré 4

par **Imod** » 30 Nov 2007, 19:00

Amusant et très facile :zen:

Pour a et b deux réels donnés , montrer que

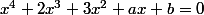
ne peut pas avoir quatre solutions réelles .

Amusez-vous bien :we:

Imod

par **ThSQ** » 30 Nov 2007, 19:09

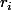
les racines

et là c'est abûsé !

par **Imod** » 30 Nov 2007, 19:31

Je voulais distraire les lycéens peu habitués à manipuler les fonctions symétriques des racines mais là , j'ai peut-être visé un peu bas : 9 minutes :hum:

Imod

par **Billball** » 30 Nov 2007, 19:44

lycéen, euuuh, de haut niveau alors :dodo:

par **Imod** » 30 Nov 2007, 20:05

Billball a écrit:lycéen, euuuh, de haut niveau alors :dodo:

Pour un exercice d'olympiade , il est très facile mais qu'un lycéen n'y arrive pas ou difficilement n'a rien d'inquiétant . J'ai déjà eu l'ocasion de dire que des "vrais" sujets d'olympiade ne devraient utiliser que des résultats et des "idées" de premières et terminales . Mais je prêche dans le désert , les auteurs des olympiades préférant des sujets techniques sur lesquels ils peuvent préparer leurs poulains . Je préfère largement les sujets des "tournois des villes" ou autres "Rallye maths" bien plus sympas et hors dressage : un avis qui n'engage que moi .

Imod

par **ThSQ** » 30 Nov 2007, 20:40

Assez d'accord avec toi Imod.
Ceci dit on apprend énormement à (essayer, même tout seul, ...) de préparer pour les olympiades.
On apprend plein de résultats qu'on ne soupçonnait même pas (arithmétique, combinatoire !!, ..) et SURTOUT on apprend à chercher.

Bref OIM, Tournoi des villes, rallye, ..... peu importe c'est toujours très formateur (ça n'est que mon avis)

par **Imod** » 30 Nov 2007, 20:50

THsQ ,

si on a compris que faire des maths c'est d'abord chercher et pas reproduire un modèle , on a fait l'essentiel , mais je crois que sur ce point nous sommes parfaitement d'accord :we:

Imod

par **_-Gaara-_** » 30 Nov 2007, 20:50

ThSQ a écrit: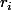les racines

et là c'est abûsé !

Respect

:++:

dis tu peux nous passer les trucs sur internet avec lesquels tu t'entraînes ? :we:

Merci (un lycéen ^^ mdr) :euh:

par **ThSQ** » 30 Nov 2007, 21:33

_-Gaara-_ a écrit:dis tu peux nous passer les trucs sur internet avec lesquels tu t'entraînes ?

Là je suis en Math Sup donc je m'entraine pas spécialement ... (trop tard

) mais ça m'amuse toujours de chercher les exos du style olympiade.

Sinon j'imagine que http://www.animath.fr/ est un bon point d'entrée.

par **lapras** » 30 Nov 2007, 22:06

Bonsoir,
ce problème est simple, en tout cas comme le dit Imod pour le niveau olympiade. Je pense vraiment qu'en 1ere S dans un contrôle (un bon controle alors !) on pourrait faire cet exercice.

par **_-Gaara-_** » 30 Nov 2007, 22:24

lapras ! te revoilà ^^ (ou me revoilà parce que moi aussi j'étais ailleurs lolll )

:we: :zen:

par **Skullkid** » 30 Nov 2007, 23:28

Je crois que c'est la première fois que je vois un sujet dans la section Olympiades qui me paraît faisable en première xD

Cela dit, si on avait donné cet exo à ma classe de première, ça aurait été l'hécatombe...Enfin, même si ces problèmes d'olympiades demandent en général, comme l'a dit Imod, des connaissances qui dépassent le cadre du lycée, je trouve que c'est quand même bien de familiariser les élèves qui ont de l'avance et de l'interêt pour la matière avec des notions et techniques un peu plus compliquées.

Personnellement j'aurais bien aimé être entraîné à ça, avant d'arriver en prépa sans savoir rien faire, face à des gars qui ont déjà pas mal entamé des notions du programme de sup...

par **ThSQ** » 01 Déc 2007, 14:10

Skullkid a écrit:Je crois que c'est la première fois que je vois un sujet dans la section Olympiades qui me paraît faisable en première xD

Vas voir ce que font nos amis marocains !
http://mathsmaroc.jeun.fr/premiere-f5/

par **Skullkid** » 01 Déc 2007, 14:31

Mon référentiel du "faisable en première" est assez inadéquat apparemment ^^

par **yos** » 02 Déc 2007, 23:20

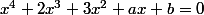
Imod a écrit:Pour a et b deux réels donnés , montrer que ne peut pas avoir quatre solutions réelles .

Et si on dit que la courbe de

est convexe et donc ne saurait rencontrer une droite en plus de 2 points on a bon?

par **Imod** » 03 Déc 2007, 11:39

yos a écrit:Et si on dit que la courbe de est convexe et donc ne saurait rencontrer une droite en plus de 2 points on a bon?

Il faut quand même se méfier des racines multiples

est convexe et a toutes ses racines réelles .

Imod

par **yos** » 03 Déc 2007, 16:54

Imod a écrit:toutes ses [une] racines réelles.

Mais la question initiale est sans ambiguité.

par **Imod** » 03 Déc 2007, 18:21

yos a écrit:Mais la question initiale est sans ambiguité.

C'est toujours ambigu quand on parle des racines multiples pour bien faire il aurait fallu préciser "quatre racines réelles distinctes" .

Imod

Polynôme de degré 4

Polynôme de degré 4

Qui est en ligne