Hypothese de récurrence : il existe une suite
)
telle que pour tout

différent de

,
, P(x_j)) = 1)
.
Soit
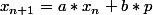
avec
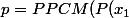, P(x_2), ... , P(x_{n-1})))
a tel que
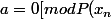])
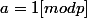

existe car
) = 1)
et d'apres le théoreme des restes chinois ce systeme admet une solution (unique modulo
)
)

un entier quelqueconque supérieur ou égal à 1.
alors
 = P(x_n) [mod p])
=>
 = u*p + r)
 = v*p + r)
donc
 = P(x_n) + p*(u-v))
tout diviseur commun à

et
)
est un diviseur commun à
)
et

donc
 , p) = PGCD(P(x_{n+1}) , p) = 1)
Il faut donc trouver b tel que
, P(x_n)) = 1)
et

sera le terme

de la suite vérifiant la propriété de récurrence.
Comme
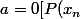])
 = P(bp) [mod P(x_n)])
On peut trouver

tel que
 = 1 [mod P(x_n)])
pour un certain coefficient h car :
on sait que pour tout
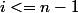
,
par bezout il existe u_i tel que :
 = 1 [P(x_n)])
comme
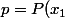*P(x_2)*...*P(x_{n-1}))
Il existe donc U tel que :
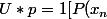])
en posant
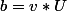
, on a
donc
 = P(v*U*p) = P(v) [P(x_n)])
si on prend
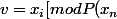], alors P(x_{n+1}) = P(v) = P(x_i))
[mod P(x_n)][/TEX] donc
 = u_i*P(x_i) = 1 [P(x_n)])
il existe
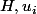
tels que
*u_i + P(x_n)*H = 1)
et grâce au théorème de bezout :
, P(x_n)) = 1)
c'est ce qu'il fallait démontrer.
Par récurrence, on construit donc la suite

les nombres premiers divisant
. On veut résoudre le systeme de congruence suivant :
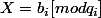
non nuls (l'existence des
est évidente)